
【题目】已知,在![]() 中,
中,![]() ,
,![]() 为
为![]() 上一动点,以
上一动点,以![]() 为斜边作
为斜边作![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() ,且
,且![]() .
.
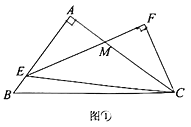
(1)如图①,若![]() 平分
平分![]() ,
,![]() ,求
,求![]() 的长
的长
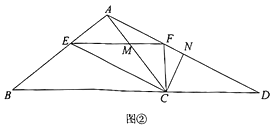
(2)如图②,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,求证
,求证![]() .
.
【答案】(1)12;(2)见解析
【解析】
(1)由“SAS”可证△AEM≌△FCM,可得EM=MC,由等腰三角形性质可求∠AEF=∠MCE=∠MEC=30°,由直角三角形的性质可求ME=MC=8,即可求AC的长;
(2)过点C作CG⊥AC交AD于点G,由“SAS”可证△ACG≌△EFC,可得AG=CE,CF=CG,由等腰三角形的性质可得FG=2FN,即可得结论.
(1)∵EF平分∠AEC,
∴∠AEF=∠FEC,
∵∠BAC=∠EFC=90°,AM=MF,∠AME=∠FMC
∴△AEM≌△FCM(SAS)
∴EM=MC
∴∠MEC=∠MCE
∴∠MEC=∠MCE=∠AEF,
∵∠MEC+∠MCE+∠AEF=90°
∴∠AEF=∠MCE=∠MEC=30°,且∠BAC=90°
∴EM=2AM=8
∴MC=8
∴AC=AM+MC=12
(2)如图,过点C作CG⊥AC交AD于点G,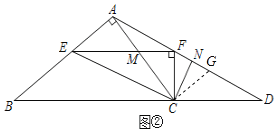
由(1)可知:EM=MC
∵AM=MF
∴AC=EF,
∵∠BAC=∠EFC=90°
∴点A,点F,点C,点E四点共圆
∴∠CAG=∠FEC,且AC=EF,∠EFC=∠ACG=90°
∴△ACG≌△EFC(ASA)
∴AG=CE,CF=CG,
∵CF=CG,CN⊥AG
∴FG=2FN
∴EC=AG=AF+FG=AF+2FN


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1)∠DCF=![]() ∠BCD;(2)EF=CF;(3)S△BEC= 2S△CEF;(4)∠DFE=3∠AEF;其中正确的结论是( )
∠BCD;(2)EF=CF;(3)S△BEC= 2S△CEF;(4)∠DFE=3∠AEF;其中正确的结论是( )
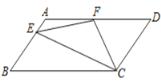
A.(1)(2)B.(1)(2)(4)C.(2)(3)(4)D.(1)(3)(4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2![]() =(1+
=(1+![]() )2,善于思考的小明进行了以下探索:
)2,善于思考的小明进行了以下探索:
设a+b=(m+n![]() )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() .
.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把部分a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m、n的式子分别表示a、b,得a= ,b= ;
)2,用含m、n的式子分别表示a、b,得a= ,b= ;
(2)试着把7+4![]() 化成一个完全平方式.
化成一个完全平方式.
(3)若a是216的立方根,b是16的平方根,试计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 分别在
分别在![]() 的边
的边![]() 上运动(不与点
上运动(不与点![]() 重合),
重合),![]() 是
是![]() 的平分线,
的平分线,![]() 的延长线交角
的延长线交角![]() 的平分线于点
的平分线于点![]() .
.

(1)若![]() ,求
,求![]() 的度数.
的度数.
(2)若![]() ,求
,求![]() 的度数.
的度数.
(3)若![]() ,请用含
,请用含![]() 的代数式表示
的代数式表示![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,BD是一条对角线,点E在直线CD上(与点C,D不重合),连接AE,平移△ADE,使点D移动到点C,得到△BCF,过点F作FG⊥BD于点G,连接AG,EG.

(1)问题猜想:如图1,若点E在线段CD上,试猜想AG与EG的数量关系是____________,位置关系是____________;
(2)类比探究:如图2,若点E在线段CD的延长线上,其余条件不变,小明猜想(1)中的结论仍然成立,请你给出证明;
(3)解决问题:若点E在线段DC的延长线上,且∠AGF=120°,正方形ABCD的边长为2,请在备用图中画出图形,并直接写出DE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 三个顶点的坐标分别为
三个顶点的坐标分别为![]() ,
,![]() ,
,![]() ,
,
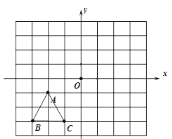
(1)若将△ABC 向右平移三个单位长度得到△A1B1C1,则点 A1 的坐标为________![]()
(2)若△ABC 与△A2B2C2 关于原点 O 成中心对称,则点 A2 的坐标________;
(3)画出△ABC 绕原点 O 顺时针旋转 90°后的对应图形△A3B3C3,并写出 A3 的坐标_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商城销售A,B两种自行车.A型自行车售价为2 100元/辆,B型自行车售价为1 750元/辆,每辆A型自行车的进价比每辆B型自行车的进价多400元,商城用80 000元购进A型自行车的数量与用64 000元购进B型自行车的数量相等.
(1)求每辆A,B两种自行车的进价分别是多少?
(2)现在商城准备一次购进这两种自行车共100辆,设购进A型自行车m辆,这100辆自行车的销售总利润为y元,要求购进B型自行车数量不超过A型自行车数量的2倍,总利润不低于13 000元,求获利最大的方案以及最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备组织七年级400名学生参加北京夏令营,已知用3辆小客车和1辆大客车每次可运送学生105人;用1辆小客车和2辆大客车每次可运送学生110人;
(1)每辆小客车和每辆大客车各能坐多少名学生?
(2)若学校计划租用小客车x辆,大客车y辆,一次送完,且恰好每辆车都坐满;
①请你设计出所有的租车方案;
②若小客车每辆需租金4000元,大客车每辆需租金7600元,请选出最省钱的租车方案,并求出最少租金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE=AC,AB=AD,∠EAB=∠CAD.
(1)BC与DE相等吗?说明理由.
(2)若BC与DE相交于点F,EF=CF.连接AF,∠BAF与∠DAF相等吗?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com