
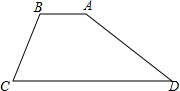
 水坝的横截面为梯形ABCD,迎水坡AD的坡角为30°,背水坡BC的坡度为1:1,坝顶宽AB为4m,坝高为6m
水坝的横截面为梯形ABCD,迎水坡AD的坡角为30°,背水坡BC的坡度为1:1,坝顶宽AB为4m,坝高为6m分析 (1)首先过B、C作BE⊥AD、CF⊥AD,可得四边形BEFC是矩形,又由背水坡AB的坡度=1:1,迎水坡CD的坡角∠ADC为30°,根据坡度的定义,即可求解,
(2)过M、N作ME⊥CD、NF⊥CD,可得四边形,MEFN是矩形,又由背水坡的坡度=1:1,迎水坡的坡角∠ADC为30°,根据坡度的定义,即可求得MN,从而求得增加的土方.
解答 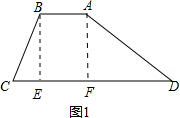 解:(1)如图1,分别过B、A作BE⊥CD、AF⊥CD,垂足为E、F,
解:(1)如图1,分别过B、A作BE⊥CD、AF⊥CD,垂足为E、F,
可得:BE∥AF,
又∵AB∥CD,
∴AB=EF BE=AF
由题意,得EF=AB=4m,BE=AF=6m,
∵背水坡BC的坡度为1:1,
∴∠BCE=45°,
∴CE=BE×cot45°=6×1=6,
DF=AF•cot30°=6×$\sqrt{3}$=6$\sqrt{3}$,
∴CD=CE+EF+DF=6+4+6$\sqrt{3}$=10+6$\sqrt{3}$
答:坝底CD的长度为(10+6$\sqrt{3}$)m.
(2)如图2,分别过M、N作ME⊥CD、NF⊥CD,垂足为E、F,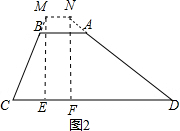
可得:ME∥NF,
又∵MN∥CD,
∴MN=EF ME=NF
由题意,得ME=NF=6.5m,
∵背水坡MC的坡度为1:1,
∴∠BCE=45°,
∴CE=ME×cot45°=6.5×1=6.5,
DF=NF•cot30°=6.5×$\sqrt{3}$=$\frac{13}{2}$$\sqrt{3}$,
∵CD=10+6$\sqrt{3}$,
∴MN=EF=10+6$\sqrt{3}$-6.5-$\frac{13}{2}$$\sqrt{3}$=3.5-$\frac{1}{2}$$\sqrt{3}$,
∴堤坝加高0.5米需要增加土方为:$\frac{1}{2}$(3.5-$\frac{1}{2}$$\sqrt{3}$+4)×0.5×1000=$\frac{1}{8}$($\sqrt{3}$+1)≈337方.
答:堤坝加高0.5米需要增加土方337方.
点评 此题考查了坡度坡角问题.此题难度适中,注意构造直角三角形,并借助于解直角三角形的知识求解是关键.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:初中数学 来源: 题型:解答题
| 打折前一次性购物总金额 | 优惠措施 |
| 不超过300元 | 不优惠 |
| 超过300元且不超过400元 | 售价打九折 |
| 超过400元 | 售价打八折 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
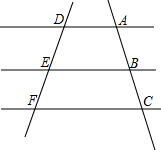 如图,已知AD∥EB∥FC,你能得到以下结论吗?说明理由.
如图,已知AD∥EB∥FC,你能得到以下结论吗?说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com