
【题目】定义:给定关于x的函数y,对于该函数图象上任意两点(x1,y1),(x2,y2),当x1=﹣x2时,都有y1=y2,称该函数为偶函数,根据以上定义,可以判断下面所给的函数中,是偶函数的有__(填上所有正确答案的序号).
①y=2x; ②y=﹣x+1; ③y=x2; ④y=﹣![]() ;
;
科目:初中数学 来源: 题型:
【题目】边长为4的正方形ABCD中,点E是BC边上的一个动点,连接DE,交AC于点N,过点D作DF⊥DE,交BA的延长线于点F,连接EF,交AC于点M.
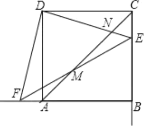
(1)判定△DFE的形状,并说明理由;
(2)设CE=x,△AMF的面积为y,求y与x之间的函数关系式;并求出当x为何值时y有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应垃圾分类处理,改善生态环境的号召,某小区将生活垃圾分成四类:厨余垃圾、可回收垃圾、不可回收垃圾、有害垃圾,分别记为a、b、c、![]() 并且设置了相应的垃圾箱:“厨余垃圾”箱,“可回收垃圾”箱,“不可回收垃圾”箱,“有害垃圾”箱,分别记为A,B,C,D.
并且设置了相应的垃圾箱:“厨余垃圾”箱,“可回收垃圾”箱,“不可回收垃圾”箱,“有害垃圾”箱,分别记为A,B,C,D.
![]() 如果将一袋有害垃圾任意投放进垃圾箱,则投放正确的概率是________.
如果将一袋有害垃圾任意投放进垃圾箱,则投放正确的概率是________.
![]() 小明将家里的厨余垃圾、可回收垃圾分装在两个袋中,任意投放在其中两个垃圾箱中,用画树状图或列表的方法求这两袋垃圾都投放正确的概率.
小明将家里的厨余垃圾、可回收垃圾分装在两个袋中,任意投放在其中两个垃圾箱中,用画树状图或列表的方法求这两袋垃圾都投放正确的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,l是经过A(2,0),B(0,b)两点的直线,且b0,点C的坐标为(2,0),当点B移动时,过点C作CD⊥l交于点D.
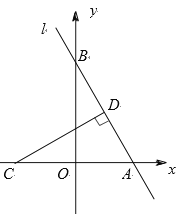
(1)求点D,O之间的距离;
(2)当tan∠CDO=![]() 时,求直线l的解析式;
时,求直线l的解析式;
(3)在(2)的条件下,直接写出△ACD与△AOB重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展以“学习朱子文化,弘扬理学思想”为主题的读书月活动,并向学生征集读后感,学校将收到的读后感篇数按年级进行统计,绘制了以下两幅统计图(不完整).
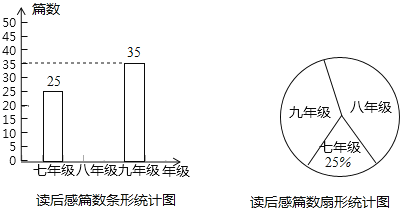
据图中提供的信息完成以下问题
(1)扇形统计图中“八年级”对应的圆心角是 °,并补全条形统计图;
(2)经过评审,全校有4篇读后感荣获特等奖,其中有一篇来自七年级,学校准备从特等奖读后感中任选两篇在校广播电台上播出,请利用画树状图或列表的方法求出七年级特等奖读后感被校广播电台播出的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设抛物线y=ax2+bx+c与x轴交于两个不同的点A(﹣1,0),B(m,0),与y轴交于点C(0,﹣2),且∠ACB=90度.
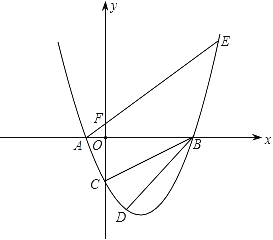
(1)求m的值和抛物线的解析式;
(2)已知点D(1,n)在抛物线上,过点A的直线y=x+1交抛物线于另一点E,求点D和点E的坐标;
(3)在x轴上是否存在点P,使以点P,B,D为顶点的三角形与三角形AEB相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为倡导节能环保,降低能源消耗,提倡环保型新能源开发,造福社会.某公司研发生产一种新型智能环保节能灯,成本为每件40元.市场调查发现,该智能环保节能灯每件售价y(元)与每天的销售量为x(件)的关系如图,为推广新产品,公司要求每天的销售量不少于1000件,每件利润不低于5元.
(1)求每件销售单价y(元)与每天的销售量为x(件)的函数关系式并直接写出自变量x的取值范围;
(2)设该公司日销售利润为P元,求每天的最大销售利润是多少元?
(3)在试销售过程中,受国家政策扶持,毎销售一件该智能环保节能灯国家给予公司补贴m(m≤40)元.在获得国家每件m元补贴后,公司的日销售利润随日销售量的增大而增大,则m的取值范围是 (直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=![]() x2―mx―n的图像与坐标轴交于A、B、C三点,其中A点的坐标为
x2―mx―n的图像与坐标轴交于A、B、C三点,其中A点的坐标为![]() 、点B的坐标是
、点B的坐标是![]() .
.
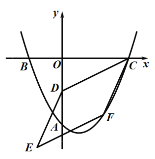
(1)求该二次函数的表达式及点C的坐标;
(2)若点D的坐标是![]() ,点F为该二次函数在第四象限内图像上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF.设平行四边形CDEF的面积为S.
,点F为该二次函数在第四象限内图像上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF.设平行四边形CDEF的面积为S.
①求S的最大值;
②在点F的运动过程中,当点E落在该二次函数图像上时,请求出点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“全民防控新冠病毒”期间某公司推出一款消毒产品,成本价8元/千克,经过市场调查,该产品的日销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)之间满足一次函数关系,该产品的日销售量与销售单价几组对应值如表:
(元/千克)之间满足一次函数关系,该产品的日销售量与销售单价几组对应值如表:
销售单价 | 12 | 16 | 20 | 24 |
日销售量 | 220 | 180 | 140 |
|
(注:日销售利润![]() 日销售量
日销售量![]() (销售单价
(销售单价![]() 成本单价)
成本单价)
(1)求![]() 关于
关于![]() 的函数解析式(不要求写出
的函数解析式(不要求写出![]() 的取值范围);
的取值范围);
(2)根据以上信息,填空:
①![]() _______千克;
_______千克;
②当销售价格![]() _______元时,日销售利润
_______元时,日销售利润![]() 最大,最大值是_______元;
最大,最大值是_______元;
(3)该公司决定从每天的销售利润中捐赠100元给“精准扶贫”对象,为了保证捐赠后每天的剩余利润不低于1500元,试确定该产品销售单价的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com