
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���y��![]() x2�Dmx�Dn��ͼ���������ύ��A��B��C���㣬����A�������Ϊ
x2�Dmx�Dn��ͼ���������ύ��A��B��C���㣬����A�������Ϊ![]() ����B��������
����B��������![]() ��
��
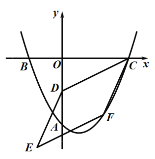
(1)��ö��κ����ı���ʽ����C�����ꣻ
(2)����D��������![]() ����FΪ�ö��κ����ڵ���������ͼ���ϵĶ��㣬����CD��CF����CD��CFΪ�ڱ���ƽ���ı���CDEF����ƽ���ı���CDEF�����ΪS��
����FΪ�ö��κ����ڵ���������ͼ���ϵĶ��㣬����CD��CF����CD��CFΪ�ڱ���ƽ���ı���CDEF����ƽ���ı���CDEF�����ΪS��
����S�����ֵ��
���ڵ�F���˶������У�����E���ڸö��κ���ͼ����ʱ���������E�����꣮
���𰸡���1��![]() ����8��0������2����50����
����8��0������2����50����![]()
��������
��1����A���B�����������κ���y��![]() x2�Dmx�Dn�õ�����b��c�ķ����飬�ⷽ�������b��c���ɵõ������ߵĽ���ʽ��Ȼ����㵱y=0ʱ����Ӧ��x��ֵ���ɵõ�C�����ꣻ
x2�Dmx�Dn�õ�����b��c�ķ����飬�ⷽ�������b��c���ɵõ������ߵĽ���ʽ��Ȼ����㵱y=0ʱ����Ӧ��x��ֵ���ɵõ�C�����ꣻ
��2��������OF��FD����ͼ��F(t,![]() )������S=2S��CDF=2(S�ı���CFDO-S��CDO)�����÷ָ���S�ı���CFDO�����������������ʽ���S��CDO���õ�S=
)������S=2S��CDF=2(S�ı���CFDO-S��CDO)�����÷ָ���S�ı���CFDO�����������������ʽ���S��CDO���õ�S=![]() �����ö��κ��������ʵõ���t=3ʱ��S�����ֵ�����ֵΪ50��
�����ö��κ��������ʵõ���t=3ʱ��S�����ֵ�����ֵΪ50��
�������ı���CDEF��ƽ���ı��Σ��õ�CD��EF��CD=EF������C���D��������������жϵ�C����ƽ��4����λ��������ƽ��8����λ�õ��˵�D�����F����ƽ��4����λ��������ƽ��8����λ�õ��˵�E������E(t-8,![]() )��Ȼ��ѵ�E(t-8,
)��Ȼ��ѵ�E(t-8,![]() )���������߽���ʽ�õ�����t�ķ��̣��ٽⷽ�����t�ɣ�
)���������߽���ʽ�õ�����t�ķ��̣��ٽⷽ�����t�ɣ�
�⣺��1�����κ���y��![]() x2�Dmx�Dn��ͼ���A(0��-8)��B(-4��0)
x2�Dmx�Dn��ͼ���A(0��-8)��B(-4��0)
��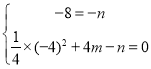
���![]()
����κ�������ʽΪ![]()
��y=0�����![]()
���C������Ϊ(8,0)
��2��������OF��FD����ͼ��F(t,![]() )
)
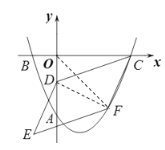
���ı���CDEF��ƽ���ı���
��S=2S��CDF=2(S�ı���CFDO-S��CDO)
S�ı���CFDO=S��OCF+S��ODF![]()
S��CDO=![]() ��8��4=16
��8��4=16
��S=2S��CDF=2(![]() -16)=
-16)= ![]() =
=![]()
��t=3ʱ��S�����ֵ�����ֵΪ50��
�ڡ��ı���CDEF��ƽ���ı���
��CD��EF��CD=EF
�ߵ�C����ƽ��4����λ��������ƽ��8����λ�õ��˵�D
���F����ƽ��4����λ��������ƽ��8����λ�õ��˵�E
����E(t-8,![]() )���ֵ�E����������
)���ֵ�E����������
��![]() =
=![]() (t-8)2-(t-8)-8
(t-8)2-(t-8)-8
���t=7
��E(-1,![]() )
)
�ʴ�Ϊ��1��![]() ����8��0������2����50����E(-1,
����8��0������2����50����E(-1,![]() )
)



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��![]() ��
��![]() �����Բ��
�����Բ��![]() Ϊֱ����
Ϊֱ����![]() ��ƽ���߽�O�ڵ�D������D��
��ƽ���߽�O�ڵ�D������D��![]() ���ֱ�
���ֱ�![]() ��
��![]() ���ӳ����ڵ�E��F��
���ӳ����ڵ�E��F��
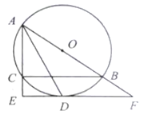
��1����֤��![]() ��
��![]() �����ߣ�
�����ߣ�
��2����գ�
�ٵ�![]() �Ķ���Ϊ_________ʱ���ı���
�Ķ���Ϊ_________ʱ���ı���![]() Ϊ���Σ�
����
����![]() �İ뾶Ϊ
�İ뾶Ϊ![]() ��
��![]() ����
����![]() �ij�Ϊ_________��
�ij�Ϊ_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��������x�ĺ���y�����ڸú���ͼ�����������㣨x1��y1������x2��y2������x1����x2ʱ������y1��y2���Ƹú���Ϊż�������������϶��壬�����ж����������ĺ����У���ż��������__������������ȷ�𰸵���ţ���
��y��2x�� ��y����x+1�� ��y��x2�� ��y����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼA��B��C�ڡ�O�ϣ�����OA��OB��OC������BOC��3��AOB���ӻ�AC�Ķ�����120o��OC��![]() ����ͼ����Ӱ���ֵ������ ( )
����ͼ����Ӱ���ֵ������ ( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����4����ͬ��Сֽ�����ɼס��ҡ�������4֧ǩ������һ�������У����Ⱥ��ȴӺ�����������1֧ǩ(���Ż�)���ٴ�ʣ���3֧ǩ��������1֧ǩ��
(1)С�ŵ�һ�γ鵽������ǩ�ĸ����� ��
(2)��������֧ǩ�У�1֧Ϊ��ǩ��1֧Ϊ��ǩ�ĸ���(�û���״ͼ���б������)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
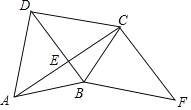
����Ŀ����ͼ���ı���ABCD�ĶԽ���AC��BD�ڵ�E��AB��BC��FΪ�ı���ABCD��һ�㣬�ҡ�FCA��90�㣬��CBF����DCB��
��1����֤���ı���DBFC��ƽ���ı��Σ�
��2�����BCƽ�֡�DBF����F��45�㣬BD��2����AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
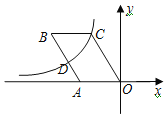
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OABC�Ķ���B��C�ڵڶ����ޣ���DΪAB�ߵ��е㣬����������y��![]() �ڵڶ�����ͼ��C��D���㣮����A�������ǣ���2
�ڵڶ�����ͼ��C��D���㣮����A�������ǣ���2![]() ��0����tan��COA��3����k��ֵΪ_____��
��0����tan��COA��3����k��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ����![]() �ύ�ڵ�A����
�ύ�ڵ�A����![]() �ύ��C��������
�ύ��C��������![]() ��A��C���㣬��x�ύ����һ��B��
��A��C���㣬��x�ύ����һ��B��
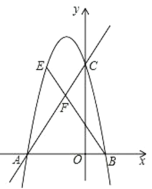
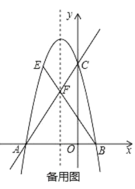
��1���������ߵĽ���ʽ��
��2����ֱ��AC�Ϸ�������������һ����E������BE����ֱ��AC�ཻ�ڵ�F����![]() ʱ����sin��EBA��ֵ��
ʱ����sin��EBA��ֵ��
��3����N�������߶Գ�����һ�㣬�ڣ�2���������£�����Eλ�ڶԳ�����࣬�����������Ƿ����һ��M��ʹ��M��N��E��BΪ������ı�����ƽ���ı��Σ������ڣ�ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
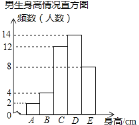
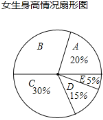
����Ŀ��ijУΪ���˽�ѧ�����������������Ը�У������Ů�������߽��г������飬��֪��ȡ�������У�������Ů����������ͬ�������������ݻ��Ƴ������ͳ��ͼ����
��� | A | B | C | D | E |
���ߣ�cm�� | x��150 | 150��x��155 | 155��x��160 | 160��x��165 | x��165 |
����ͼ������Ϣ���ش��������⣺
��1���������У��������ߵ���λ������ �飨�������ţ���Ů��������B��������� �ˣ�
��2����֪��У��������500�ˣ�Ů��480�ˣ������������155��x��165֮���ѧ��Լ�ж����ˣ�
��3��������������A��B������������2�˲μ�һ������ǡ����1����A�顢1����B��ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com