
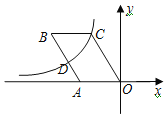
【题目】如图,在平面直角坐标系中,OABC的顶点B、C在第二象限,点D为AB边的中点,反比例函数y=![]() 在第二象限的图象经过C、D两点.若点A的坐标是(﹣2
在第二象限的图象经过C、D两点.若点A的坐标是(﹣2![]() ,0),tan∠COA=3,则k的值为_____.
,0),tan∠COA=3,则k的值为_____.
【答案】-16
【解析】
过点C作CE⊥OA于E,过点D作DF⊥x轴于F,依据△ADF∽△OCE,可得CE=2DF,OE=2AF,设OE=a,可得CE=3a,C(-a,3a),D(﹣![]() a﹣
a﹣![]() ,
,![]() a),依据反比例函数y=
a),依据反比例函数y=![]() 在第二象限的图象经过C、D两点,即可得到a的值,进而得出k的值.
在第二象限的图象经过C、D两点,即可得到a的值,进而得出k的值.
如图,过点C作CE⊥OA于E,过点D作DF⊥x轴于F,则∠AFD=∠OEC=90°,
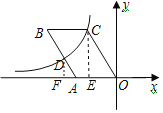
∵OC∥AB,
∴∠DAF=∠COE,
∴△ADF∽△OCE,
在![]() OABC中,OC=AB,D为边AB的中点,
OABC中,OC=AB,D为边AB的中点,
∴OC=AB=2AD,
∴CE=2DF,OE=2AF,
设OE=a,则CE=3a,C(﹣a,3a),
∴AF=![]() a,DF=
a,DF=![]() a,
a,
又∵A(![]() ,0),
,0),
∴AO=![]() ,
,
∴OF=![]() a+
a+![]() ,
,
∴D(﹣![]() a﹣
a﹣![]() ,
,![]() a),
a),
∵反比例函数y=![]() 在第二象限的图象经过C、D两点,
在第二象限的图象经过C、D两点,
∴k=﹣a3a=(﹣![]() a﹣
a﹣![]() )
)![]() a,
a,
解得a=![]() ,
,
∴k=﹣![]() ×
×![]() =﹣16
=﹣16
故答案为:﹣16


科目:初中数学 来源: 题型:
【题目】为响应垃圾分类处理,改善生态环境的号召,某小区将生活垃圾分成四类:厨余垃圾、可回收垃圾、不可回收垃圾、有害垃圾,分别记为a、b、c、![]() 并且设置了相应的垃圾箱:“厨余垃圾”箱,“可回收垃圾”箱,“不可回收垃圾”箱,“有害垃圾”箱,分别记为A,B,C,D.
并且设置了相应的垃圾箱:“厨余垃圾”箱,“可回收垃圾”箱,“不可回收垃圾”箱,“有害垃圾”箱,分别记为A,B,C,D.
![]() 如果将一袋有害垃圾任意投放进垃圾箱,则投放正确的概率是________.
如果将一袋有害垃圾任意投放进垃圾箱,则投放正确的概率是________.
![]() 小明将家里的厨余垃圾、可回收垃圾分装在两个袋中,任意投放在其中两个垃圾箱中,用画树状图或列表的方法求这两袋垃圾都投放正确的概率.
小明将家里的厨余垃圾、可回收垃圾分装在两个袋中,任意投放在其中两个垃圾箱中,用画树状图或列表的方法求这两袋垃圾都投放正确的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为倡导节能环保,降低能源消耗,提倡环保型新能源开发,造福社会.某公司研发生产一种新型智能环保节能灯,成本为每件40元.市场调查发现,该智能环保节能灯每件售价y(元)与每天的销售量为x(件)的关系如图,为推广新产品,公司要求每天的销售量不少于1000件,每件利润不低于5元.
(1)求每件销售单价y(元)与每天的销售量为x(件)的函数关系式并直接写出自变量x的取值范围;
(2)设该公司日销售利润为P元,求每天的最大销售利润是多少元?
(3)在试销售过程中,受国家政策扶持,毎销售一件该智能环保节能灯国家给予公司补贴m(m≤40)元.在获得国家每件m元补贴后,公司的日销售利润随日销售量的增大而增大,则m的取值范围是 (直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=![]() x2―mx―n的图像与坐标轴交于A、B、C三点,其中A点的坐标为
x2―mx―n的图像与坐标轴交于A、B、C三点,其中A点的坐标为![]() 、点B的坐标是
、点B的坐标是![]() .
.
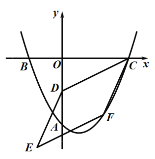
(1)求该二次函数的表达式及点C的坐标;
(2)若点D的坐标是![]() ,点F为该二次函数在第四象限内图像上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF.设平行四边形CDEF的面积为S.
,点F为该二次函数在第四象限内图像上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF.设平行四边形CDEF的面积为S.
①求S的最大值;
②在点F的运动过程中,当点E落在该二次函数图像上时,请求出点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.
(1)当每吨售价是240元时,计算此时的月销售量;
(2)在遵循“薄利多销”的原则下,问每吨材料售价为多少时,该经销店的月利润为9000元?
(3)小静说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
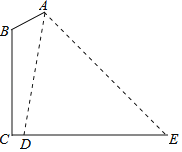
【题目】如图是某路灯在铅垂面内的示意图,灯柱BC的高为10米,灯柱BC与灯杆AB的夹角为120°.路灯采用锥形灯罩,在地面上的照射区域DE的长为13.3米,从D、E两处测得路灯A的仰角分别为α和45°,且tanα=6.求灯杆AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店老板到厂家选购![]() 、
、![]() 两种品牌的羽绒服,
两种品牌的羽绒服,![]() 品牌羽绒服每件进价比
品牌羽绒服每件进价比![]() 品牌羽绒服每件进价多
品牌羽绒服每件进价多![]() 元,若用
元,若用![]() 元购进
元购进![]() 种羽绒服的数量是用
种羽绒服的数量是用![]() 元购进
元购进![]() 种羽绒服数量的
种羽绒服数量的![]() 倍.
倍.
(1)求![]() 、
、![]() 两种品牌羽绒服每件进价分别为多少元?
两种品牌羽绒服每件进价分别为多少元?
(2)若![]() 品牌羽绒服每件售价为
品牌羽绒服每件售价为![]() 元,
元,![]() 品牌羽绒服每件售价为
品牌羽绒服每件售价为![]() 元,服装店老板决定一次性购进
元,服装店老板决定一次性购进![]() 、
、![]() 两种品牌羽绒服共
两种品牌羽绒服共![]() 件,在这批羽绒服全部出售后所获利润不低于
件,在这批羽绒服全部出售后所获利润不低于![]() 元,则最少购进
元,则最少购进![]() 品牌羽绒服多少件?
品牌羽绒服多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“全民防控新冠病毒”期间某公司推出一款消毒产品,成本价8元/千克,经过市场调查,该产品的日销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)之间满足一次函数关系,该产品的日销售量与销售单价几组对应值如表:
(元/千克)之间满足一次函数关系,该产品的日销售量与销售单价几组对应值如表:
销售单价 | 12 | 16 | 20 | 24 |
日销售量 | 220 | 180 | 140 |
|
(注:日销售利润![]() 日销售量
日销售量![]() (销售单价
(销售单价![]() 成本单价)
成本单价)
(1)求![]() 关于
关于![]() 的函数解析式(不要求写出
的函数解析式(不要求写出![]() 的取值范围);
的取值范围);
(2)根据以上信息,填空:
①![]() _______千克;
_______千克;
②当销售价格![]() _______元时,日销售利润
_______元时,日销售利润![]() 最大,最大值是_______元;
最大,最大值是_______元;
(3)该公司决定从每天的销售利润中捐赠100元给“精准扶贫”对象,为了保证捐赠后每天的剩余利润不低于1500元,试确定该产品销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春天是放风筝的好时节,小明为了让风筝顺利起飞,特地将风筝放在坡度为1:2.4的山坡上,并站在视线刚好与风筝起飞点A齐平的B处,起风后小明开始往下跑26米至坡底C处,并继续沿平地向前跑16米到达D处后站在原地开始调整,小明将手中的线轴刚好举到与视线齐平处测得风筝的仰角是37°,此时风筝恰好升高到起飞时的正上方E处.已知小明视线距地面高度为1.5米,图中风筝E、A、B、C、D五点在同一平面,则风筝上升的垂直距离AE约为( )米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
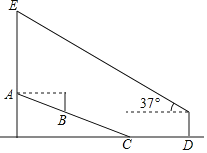
A.34.2B.32.7C.31.2D.22.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com