练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
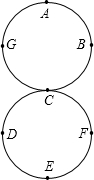
    7．如图，两个半径都是4cm的圆外切于点C，一只蚂蚁由点A开始依A、B、C、D、E、F、C、G、A的顺序沿着圆周上的8段长度相等的路径绕行，蚂蚁在这8段路径上不断爬行，直到行走2006πcm后才停下来，则蚂蚁停的那一个点为（　　）
    A．D点B．E点C．F点D．G点

    分析 首先求得蚂蚁爬行一周的路径长，则得到每一段的长，计算出爬行2006π时，爬行的圈数，即可确定．

    解答 解：根据行走一圈的周长是：2×2π×4=16π（cm），
    每相邻两点间的路程是2π，
    2006π=16π×125+6π，
    则最后停在了第4个点，即D点．
    故选：A．

    点评 本题考查了圆周长的计算，正确理解几个位置不断的循环重复是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    10．在“争创美丽校园，争做文明学生”示范校评比活动中，10位评委给某校的评分情况下表所示：
    评分（分）80859095
    评委人数1252
    则这10位评委评分的平均数是89分．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．统计显示，2013年底杭州市各类高中在校学生人数大约是11.4万人，将11.4万用科学记数法表示应为（　　）
    A．11.4×102B．1.14×103C．1.14×104D．1.14×105

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．某班45名同学某天每人的生活费用统计如表：
     生活费（元） 10 15 20 25 30
     学生人数（人） 4 10 15 10 6
    对于这45名同学这天每人的生活费用，下列说法错误的是（　　）
    A．平均数是20B．众数是20C．中位数是20D．极差是20

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．在△ABC中，CD⊥AB于D，若AC≠BC，∠A=32°，且$\frac{A{C}^{2}}{B{C}^{2}}$=$\frac{AD}{BD}$，则∠ABC为58或122°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

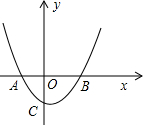    12．如图，已知在平面直角坐标系xOy中，抛物线y=ax2-2ax-4与x轴交于A、B两点，与y轴相交于点C，其中点A的坐标为（-3．，0），点D在线段AB上，AD=AC．
    （1）求这条抛物线的关系式，并求出抛物线的对称轴；
    （2）如果以DB为半径的圆D与圆C外切，求圆C的半径；
    （3）设点M在线段AB上，点N在线段BC上，如果线段MN被直线CD垂直平分，求$\frac{BN}{CN}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．如图，等圆⊙O1和⊙O2相交于A、B两点，⊙O1经过⊙O2的圆心O2，连接AO1，并延长交⊙O1于点C，则∠ACO2的度数为（　　）
    A．60°B．45°C．30°D．20°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

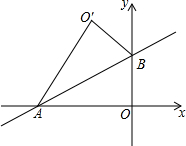    16．如图，直线y=$\frac{\sqrt{3}}{3}$x+2与x轴，y轴分别交于A，B两点，把△AOB沿着直线AB翻折后得到△AO′B，则点O′的坐标是（　　）
    A．（-$\sqrt{3}$，3）B．（$\sqrt{3}$，$\sqrt{3}$）C．（2，2$\sqrt{3}$）D．（2$\sqrt{3}$，4）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，抛物线y=ax2+c（a≠0）与y轴交于点A，与x轴交于B，C两点（点C在x轴正半轴上），△ABC为等腰直角三角形，且面积为4，现将抛物线沿BA方向平移，平移后的抛物线过点C时，与x轴的另一点为E，其顶点为F，对称轴与x轴的交点为H．
    （1）求a、c的值．
    （2）连接OF，试判断△OEF是否为等腰三角形，并说明理由．
    （3）现将一足够大的三角板的直角顶点Q放在射线AF或射线HF上，一直角边始终过点E，另一直角边与y轴相交于点P，是否存在这样的点Q，使以点P、Q、E为顶点的三角形与△POE全等？若存在，求出点Q的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案