
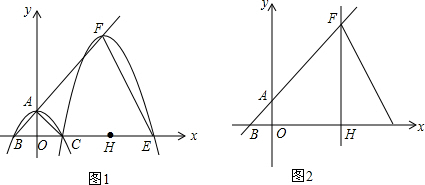
分析 (1)先求出A(0,c),则OA=c,再根据等腰直角三角形的性质得OA=OB=OC=c,理由三角形面积公式得$\frac{1}{2}$•c•2c=4,解得c=2,接着把C(2,0)代入y=ax2+2可求出a的值;
(2)如图1,先利用待定系数法求出直线AB的解析式为y=x+2,设F(t,t+2),利用抛物线平移的规律可设平移后的抛物线解析式为y=-$\frac{1}{2}$(x-t)2+t+2,再把C(2,0)代入得-$\frac{1}{2}$(2-t)2+t+2=0,可解得t=6,则平移后的抛物线解析式为y=-$\frac{1}{2}$(x-6)2+8,所以F(6,8),利用勾股定理计算出OF=10,接着根据抛物线与x轴的交点问题确定E(10,0),则OE=OF=10,于是可判断△OEF为等腰三角形;
(3)分类讨论:当点Q在射线HF上,如图2,利用三角形全等的判定方法,当EQ=EO=10时,△EQP≌△EOP,则可根据勾股定理计算出QH=2$\sqrt{21}$,于是可得Q点坐标为(6,2$\sqrt{21}$);当点Q在射线AF上,如图3,利用三角形全等的判定方法,当EQ=EO=10时,△EQP≌△EOP,设Q(m,m+2),利用两点间的距离公式得到(m-10)2+(m+2)2=102,解方程求出m的值即可得到Q点坐标.
解答 解:(1)∵抛物线y=ax2+c(a≠0)与y轴交于点A,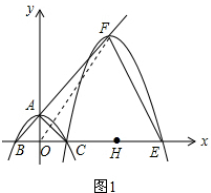
∴A(0,c),则OA=c,
∵△ABC为等腰直角三角形,
∴OA=OB=OC=c,
∴$\frac{1}{2}$•c•2c=4,解得c=2,
∴C(2,0),
把C(2,0)代入y=ax2+2得4a+2=0,解得a=-$\frac{1}{2}$;
(2)△OEF是等腰三角形.理由如下:如图1,
设直线AB的解析式为y=kx+b,
把A(0,2)、B(-2,0)代入得$\left\{\begin{array}{l}{b=2}\\{-2k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$,
则直线AB的解析式为y=x+2,
设F(t,t+2),
∵抛物线y=-$\frac{1}{2}$x2+2沿BA方向平移,平移后的抛物线过点C时,顶点为F,
∴平移后的抛物线解析式为y=-$\frac{1}{2}$(x-t)2+t+2,
把C(2,0)代入得-$\frac{1}{2}$(2-t)2+t+2=0,解得t1=0(舍去),t2=6,
∴平移后的抛物线解析式为y=-$\frac{1}{2}$(x-6)2+8,
∴F(6,8),
∴OF=$\sqrt{{6}^{2}+{8}^{2}}$=10,
令y=0,-$\frac{1}{2}$(x-6)2+8=0,解得x1=2,x2=10,
∴OE=10,
∴OE=OF,
∴△OEF为等腰三角形;
(3)存在.点Q的位置分两种情形.
情形一:点Q在射线HF上,
当点P在x轴上方时,如图2,
∵∠EQP=90°,EP=EP,
∴当EQ=EO=10时,△EQP≌△EOP,
而HE=10-6=4,
∴QH=$\sqrt{1{0}^{2}-{4}^{2}}$=2$\sqrt{21}$,
此时Q点坐标为(6,2$\sqrt{21}$);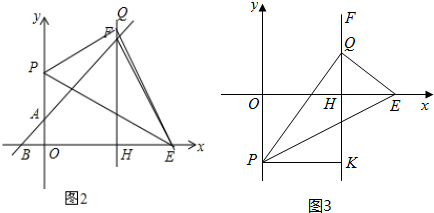
当点P在x轴下方时,如图3,有PQ=OE=10,过P点作PK⊥HF于点K,则有PK=6,
在Rt△PQK中,QK=$\sqrt{{PQ}^{2}-P{K}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∵∠PQE=90°,∴∠PQK+HQE=90°,
∵∠PKQ=∠QHE=90°,
∴△PKQ∽△QHE,
∴$\frac{PK}{QH}=\frac{QK}{HE}$,∴$\frac{6}{QH}=\frac{8}{4}$,解得QH=3,
∴Q(6,3).
情形二、点Q在射线AF上,
当PQ=OE=10时,如图4,有QE=PO,
∴四边形POEQ为矩形,∴Q的横坐标为10,
当x=10时,y=x+2=12,∴Q(10,12).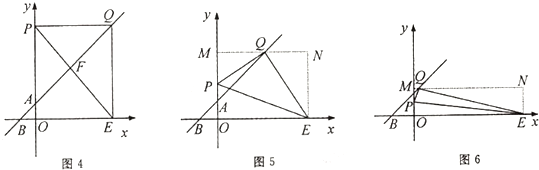
当QE=OE=10时,如图5,
过Q作QM⊥y轴于点M,过E点作x轴的垂线交QM于点N.
设Q的坐标为为(x,x+2),∴MQ=x,QN=10-x,EN=x+2,
在Rt△QEN中,有QE2=QN2+EN2,即102=(10-x)2+(x+2)2,解得x=4±$\sqrt{14}$,
当x=4+$\sqrt{14}$时,如图5,y=x+2=6+$\sqrt{14}$,∴Q(4+$\sqrt{14}$,6+$\sqrt{14}$),
当x=4-$\sqrt{14}$时,如图5,y=x+2=6-$\sqrt{14}$,∴Q(4-$\sqrt{14}$,6-$\sqrt{14}$),
综上所述,Q点的坐标为(6,2$\sqrt{21}$)或(6,3)或(10,12)或(4+$\sqrt{14}$,6+$\sqrt{14}$)或(4-$\sqrt{14}$,6-$\sqrt{14}$),使P,Q,E三点为顶点的三角形与△POE全等.
点评 本题考查了二次函数的综合题:熟练掌握二次函数的性质、二次函数平移的规律和三角形全等的判定与性质;会利用待定系数法求函数解析式;记住两点间的距离公式.


科目:初中数学 来源: 题型:选择题
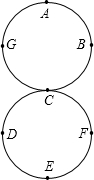 如图,两个半径都是4cm的圆外切于点C,一只蚂蚁由点A开始依A、B、C、D、E、F、C、G、A的顺序沿着圆周上的8段长度相等的路径绕行,蚂蚁在这8段路径上不断爬行,直到行走2006πcm后才停下来,则蚂蚁停的那一个点为( )
如图,两个半径都是4cm的圆外切于点C,一只蚂蚁由点A开始依A、B、C、D、E、F、C、G、A的顺序沿着圆周上的8段长度相等的路径绕行,蚂蚁在这8段路径上不断爬行,直到行走2006πcm后才停下来,则蚂蚁停的那一个点为( )| A. | D点 | B. | E点 | C. | F点 | D. | G点 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
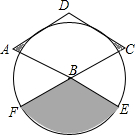 如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )
如图,菱形ABCD的边长为2,∠A=60°,以点B为圆心的圆与AD、DC相切,与AB、CB的延长线分别相交于点E、F,则图中阴影部分的面积为( )| A. | $\sqrt{3}$+$\frac{π}{2}$ | B. | $\sqrt{3}$+π | C. | $\sqrt{3}$-$\frac{π}{2}$ | D. | 2$\sqrt{3}$+$\frac{π}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
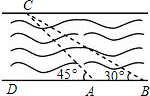 如图所示,我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度.小宇同学在A处观测对岸C点,测得∠CAD=45°,小英同学在距A处50米远的B处测得∠CBD=30°,请你根据这些数据算出河宽.(精确到0.01米,参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图所示,我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度.小宇同学在A处观测对岸C点,测得∠CAD=45°,小英同学在距A处50米远的B处测得∠CBD=30°,请你根据这些数据算出河宽.(精确到0.01米,参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
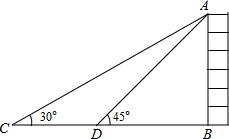 如图,某校数学兴趣小组为测得大厦AB的高度,在大厦前的平地上选择一点C,测得大厦顶端A的仰角为30°,再向大厦方向前进80米,到达点D处(C、D、B三点在同一直线上),又测得大厦顶端A的仰角为45°,请你计算该大厦的高度.(精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,某校数学兴趣小组为测得大厦AB的高度,在大厦前的平地上选择一点C,测得大厦顶端A的仰角为30°,再向大厦方向前进80米,到达点D处(C、D、B三点在同一直线上),又测得大厦顶端A的仰角为45°,请你计算该大厦的高度.(精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com