
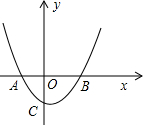
 如图,已知在平面直角坐标系xOy中,抛物线y=ax2-2ax-4与x轴交于A、B两点,与y轴相交于点C,其中点A的坐标为(-3.,0),点D在线段AB上,AD=AC.
如图,已知在平面直角坐标系xOy中,抛物线y=ax2-2ax-4与x轴交于A、B两点,与y轴相交于点C,其中点A的坐标为(-3.,0),点D在线段AB上,AD=AC.分析 (1)把点A的坐标代入函数解析式,利用方程求得a的值;然后利用抛物线解析式来求对称轴方程;
(2)根据抛物线解析式可以求得点B、C的坐标,结合已知条件“AD=AC”可以得到点D的坐标,由点的坐标与图形的性质来求圆C的半径;
(3)利用等腰△ACD、线段垂直平分线的性质得到∠AMC=∠BND,然后由三角形内角和推知∠180°-∠ACM-∠AMC=180°-∠B-∠BND,则∠A=∠BDN,易得DN∥AC,所以,根据平行线分线段成比例求得$\frac{BN}{CN}$=$\frac{BD}{AD}$=$\frac{3}{5}$.
解答 解:(1)把(-3,0)代入y=ax2-2ax-4得:9a+6a-4=0,
解得:a=$\frac{4}{15}$,
则抛物线的解析式是:y=$\frac{4}{15}$x2-$\frac{8}{15}$x-4,
对称轴是x=-$\frac{-\frac{8}{15}}{2×\frac{4}{15}}$=1,即x=1;
(2)在y=$\frac{4}{15}$x2-$\frac{8}{15}$x-4中,令y=0,得$\frac{4}{15}$x2-$\frac{8}{15}$x-4=0,
解得:x=-3或5.
则B的坐标是(5,0).
在y=$\frac{4}{15}$x2-$\frac{8}{15}$x-4中令x=0,
解得:y=-4,则C的坐标是(0,-4).
AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
则D的坐标是(2,0),
∴CD=2$\sqrt{5}$,BD=3.
当两圆外切时,RC+BD=CD,RC=2$\sqrt{5}$-3.
则圆C的半径是:2$\sqrt{5}$-3;
(3)∵AC=AD,
∴∠ADC=∠ACD,
又∵线段MN被直线CD垂直平分,
∴∠DCB=∠DCM,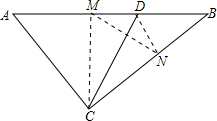
∴∠ACM=∠B.
又∵∠DNC=∠DMC,
∴∠AMC=∠BND,
∴∠180°-∠ACM-∠AMC=180°-∠B-∠BND,
∴∠A=∠BDN,
∴DN∥AC,
∴$\frac{BN}{CN}$=$\frac{BD}{AD}$=$\frac{3}{5}$.
点评 本题着重考查了待定系数法求二次函数解析式、等腰三角形判定和性质、点的坐标与图形的性质以及线段垂直平分线的性质等知识点,综合性强,考查学生数形结合的数学思想方法.(3)中弄清DN∥AC是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
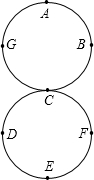 如图,两个半径都是4cm的圆外切于点C,一只蚂蚁由点A开始依A、B、C、D、E、F、C、G、A的顺序沿着圆周上的8段长度相等的路径绕行,蚂蚁在这8段路径上不断爬行,直到行走2006πcm后才停下来,则蚂蚁停的那一个点为( )
如图,两个半径都是4cm的圆外切于点C,一只蚂蚁由点A开始依A、B、C、D、E、F、C、G、A的顺序沿着圆周上的8段长度相等的路径绕行,蚂蚁在这8段路径上不断爬行,直到行走2006πcm后才停下来,则蚂蚁停的那一个点为( )| A. | D点 | B. | E点 | C. | F点 | D. | G点 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
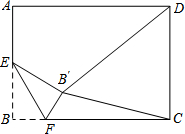 如图所示,在矩形ABC中,AB=4,AD=4$\sqrt{2}$,E是线段AB的中点,F是线段BC上的动点,△BEF沿直线EF翻折到△B′EF,连结DB′,B′C.当DB′最短时,则sin∠B′CF=$\frac{\sqrt{3}}{3}$.
如图所示,在矩形ABC中,AB=4,AD=4$\sqrt{2}$,E是线段AB的中点,F是线段BC上的动点,△BEF沿直线EF翻折到△B′EF,连结DB′,B′C.当DB′最短时,则sin∠B′CF=$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
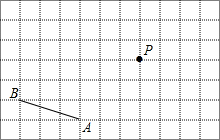 如图,在7×11网格中,已知线段AB和点P,按下列要求画图.
如图,在7×11网格中,已知线段AB和点P,按下列要求画图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
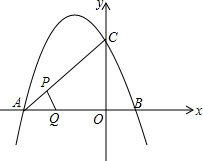 如图,二次函数y=-$\frac{4}{3}$x2-$\frac{8}{3}$x+4的图象与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿线段AC,AB运动,其中一点到达端点时,另一点也随之停止运动.
如图,二次函数y=-$\frac{4}{3}$x2-$\frac{8}{3}$x+4的图象与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿线段AC,AB运动,其中一点到达端点时,另一点也随之停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
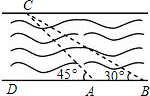 如图所示,我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度.小宇同学在A处观测对岸C点,测得∠CAD=45°,小英同学在距A处50米远的B处测得∠CBD=30°,请你根据这些数据算出河宽.(精确到0.01米,参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图所示,我市某中学课外活动小组的同学利用所学知识去测量釜溪河沙湾段的宽度.小宇同学在A处观测对岸C点,测得∠CAD=45°,小英同学在距A处50米远的B处测得∠CBD=30°,请你根据这些数据算出河宽.(精确到0.01米,参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com