
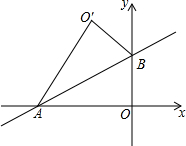
 如图,直线y=$\frac{\sqrt{3}}{3}$x+2与x轴,y轴分别交于A,B两点,把△AOB沿着直线AB翻折后得到△AO′B,则点O′的坐标是( )
如图,直线y=$\frac{\sqrt{3}}{3}$x+2与x轴,y轴分别交于A,B两点,把△AOB沿着直线AB翻折后得到△AO′B,则点O′的坐标是( )| A. | (-$\sqrt{3}$,3) | B. | ($\sqrt{3}$,$\sqrt{3}$) | C. | (2,2$\sqrt{3}$) | D. | (2$\sqrt{3}$,4) |
分析 连接OO′,交AB于点D,作O′E⊥y轴,交y于点E,由直线y=$\frac{\sqrt{3}}{3}$x+2与x轴、y轴分别交于A、B两点,求出B(0,2),A(-2$\sqrt{3}$,0),首先求出OA、OB、OO′长,进而证明△OAB∽△EO′O,求出OE、O′E的长即可解决问题.
解答 解:如图,连接OO′,交AB于点D,作O′E⊥y轴,交y于点E,由题意得:OD=O′D,OO′⊥AB;
由直线y=$\frac{\sqrt{3}}{3}$x+2与x轴、y轴分别交于A、B两点,B(0,2),A(-2$\sqrt{3}$,0),
∴OA=2$\sqrt{3}$,OB=2;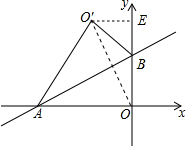
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=4,
由面积公式:$\frac{1}{2}$OA•OB=$\frac{1}{2}$AB•OD,
∴OD=$\sqrt{3}$,
∴OO′=2OD=2$\sqrt{3}$;
∵OO′⊥AB,OA⊥OB,
∴∠OBA=∠O′OE,∠BOA=∠OEO′,
∴△OAB∽△EOO′,
∴$\frac{AB}{OO′}=\frac{OB}{O′E}=\frac{OA}{OE}$,
∴O′E=$\sqrt{3}$,OE=3,
∴点O′坐标为(-$\sqrt{3}$,3).
故选:A.
点评 该题以直角坐标系为载体,以翻折变换为方法,以相似三角形的判定及其性质的应用为考查的核心构造而成;对综合的分析问题、解决问题的能力提出了较高的要求.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
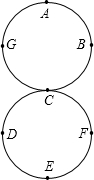 如图,两个半径都是4cm的圆外切于点C,一只蚂蚁由点A开始依A、B、C、D、E、F、C、G、A的顺序沿着圆周上的8段长度相等的路径绕行,蚂蚁在这8段路径上不断爬行,直到行走2006πcm后才停下来,则蚂蚁停的那一个点为( )
如图,两个半径都是4cm的圆外切于点C,一只蚂蚁由点A开始依A、B、C、D、E、F、C、G、A的顺序沿着圆周上的8段长度相等的路径绕行,蚂蚁在这8段路径上不断爬行,直到行走2006πcm后才停下来,则蚂蚁停的那一个点为( )| A. | D点 | B. | E点 | C. | F点 | D. | G点 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
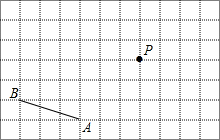 如图,在7×11网格中,已知线段AB和点P,按下列要求画图.
如图,在7×11网格中,已知线段AB和点P,按下列要求画图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
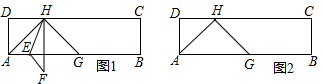
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
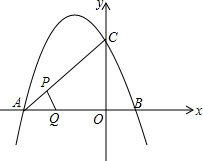 如图,二次函数y=-$\frac{4}{3}$x2-$\frac{8}{3}$x+4的图象与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿线段AC,AB运动,其中一点到达端点时,另一点也随之停止运动.
如图,二次函数y=-$\frac{4}{3}$x2-$\frac{8}{3}$x+4的图象与x轴交于A,B两点(点B在点A的右侧),与y轴交于点C,若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿线段AC,AB运动,其中一点到达端点时,另一点也随之停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
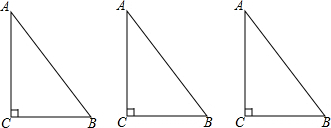
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com