
����Ŀ����ͼ��ʾ������ABC�У�![]() ��D��E�ֱ��DZ�AB��BC�ϵĶ��㣬��
��D��E�ֱ��DZ�AB��BC�ϵĶ��㣬��![]() ������AD��AE����M��N��P�ֱ���CD��AE��AC���е㣬��
������AD��AE����M��N��P�ֱ���CD��AE��AC���е㣬��![]() ��
��
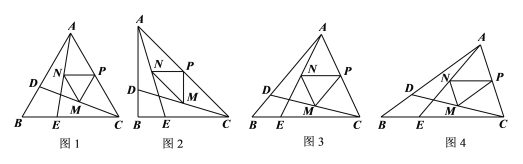
��1���۲����
������![]() ��ֵʱ��С�����ô����һ��ķ���������
��ֵʱ��С�����ô����һ��ķ���������![]() ������˼·���£�
������˼·���£�
��ͼ1������![]() ���õ�
���õ�![]() ��������λ�ߵ����ʵõ�
��������λ�ߵ����ʵõ�![]() ��
��
![]() �������ó���PMNΪ�ȱ������Σ���
�������ó���PMNΪ�ȱ������Σ���![]() ��
��
����ͼ2����![]() ������С����˼·��
������С����˼·��![]() ��ֵ��
��ֵ��
��2��̽��֤��
��ͼ3���Բ���![]() ��ֵ�Ƿ���
��ֵ�Ƿ���![]() �Ķ����йأ����йأ����ú�
�Ķ����йأ����йأ����ú�![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��![]() �����أ���˵�����ɣ�
�����أ���˵�����ɣ�
��3����չӦ��
��ͼ4��![]() ����D��E�ֱ�������AB��CB�ϵĶ��㣬��
����D��E�ֱ�������AB��CB�ϵĶ��㣬��![]() ����M��N��P�ֱ����߶�CD��AE��AC���е㣬��
����M��N��P�ֱ����߶�CD��AE��AC���е㣬��![]() ʱ����ֱ��д��MN�ij���
ʱ����ֱ��д��MN�ij���
���𰸡���1����![]() ����2��
����2��![]() ��ֵ��
��ֵ��![]() �Ķ����йأ�
�Ķ����йأ�![]() ����3��MN�ij�Ϊ
����3��MN�ij�Ϊ![]() ��
��![]() ��
��
��������
��1�����ȸ����߶εĺͲ����![]() ���ٸ�����λ�߶�����ƽ���ߵ����ʵó�
���ٸ�����λ�߶�����ƽ���ߵ����ʵó�![]() ���Ӷ��ɵó�
���Ӷ��ɵó�![]() ��Ȼ����ݵ���ֱ�������ε����ʼ��ɵã�
��Ȼ����ݵ���ֱ�������ε����ʼ��ɵã�
��2�������⣨1���ķ������ó�![]() Ϊ���������κ�
Ϊ���������κ�![]() �Ķ����������õ��������ε����ʼ�������𰸣�
�Ķ����������õ��������ε����ʼ�������𰸣�
��3�����������������D��E�ֱ��DZ�AB��CB�ϵĶ���ʱ�͵���D��E�ֱ��DZ�AB��CB���ӳ����ϵĶ���ʱ����ͼ�����������������õ��������ε��������ж��ó�![]() ���ٸ������������ε��ж������ʵó�BC��CE�ij����ɸ��ݵ��������ε����ߺ�һ�Եó�
���ٸ������������ε��ж������ʵó�BC��CE�ij����ɸ��ݵ��������ε����ߺ�һ�Եó�![]() ���Ӷ��ɵ�
���Ӷ��ɵ�![]() ��ֵ�����ֱ����ã�2���Ľ��ۼ��ɵ�MN�ij���
��ֵ�����ֱ����ã�2���Ľ��ۼ��ɵ�MN�ij���
��1����![]()
��![]()
![]()
��![]() Ϊ����ֱ�������Σ�
Ϊ����ֱ�������Σ�![]()
�ߵ�M��N��P�ֱ���CD��AE��AC���е�
![]()
![]()
��![]()
��![]() Ϊ����ֱ�������Σ�
Ϊ����ֱ�������Σ�
��![]()
��![]() ��
��
��2��![]() ��ֵ��
��ֵ��![]() �Ķ����йأ����������£�
�Ķ����йأ����������£�
�ɣ�1����֪��![]() ����
����![]() ����������
����������
![]()
��ͼ5����![]()
��![]()
��![]() ��
��![]() ����
����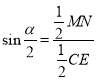
��![]() ��
��
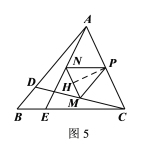
��3�������⣬���������������
�ٵ���D��E�ֱ��DZ�AB��CB�ϵĶ���ʱ
��ͼ6����![]() �Ľ�ƽ���߽�AB���ڵ�F��������BP
�Ľ�ƽ���߽�AB���ڵ�F��������BP
![]()
![]()
![]()
![]()
![]() ��
��![]()
![]() ����
����![]()
��![]() ����
����![]()
![]()
���![]() ��
��![]() ���������⣬��ȥ��
���������⣬��ȥ��
��![]()
![]()
�ɣ�2����֪��![]()
![]()
![]() ��P��AC�ϵ��е�
��P��AC�ϵ��е�
![]() ��
��![]() �����������ε����ߺ�һ��
�����������ε����ߺ�һ��
��![]() ��
��![]() ����
����![]()
![]()
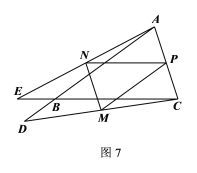
����ͼ7������D��E�ֱ��DZ�AB��CB���ӳ����ϵĶ���ʱ
ͬ���ɵã�![]()
![]()
![]()
���ϣ�MN�ij�Ϊ![]() ��
��![]() ��
��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��x2+bx+c��ֱ��y��![]() x��3���ڣ�B���㣬���е�A��y���ϣ���B����Ϊ����4����5������PΪy��������������һ���㣬����P��PC��x���ڵ�C����AB�ڵ�D��
x��3���ڣ�B���㣬���е�A��y���ϣ���B����Ϊ����4����5������PΪy��������������һ���㣬����P��PC��x���ڵ�C����AB�ڵ�D��
��1���������߶�Ӧ�ĺ�������ʽ��
��2����O��A��P��DΪ�����ƽ���ı����Ƿ���������ڣ����P�����ꣻ�������ڣ�˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
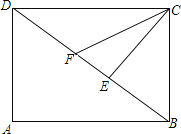
����Ŀ����ͼ������ABCD�У�CE��BD��E��CFƽ�֡�DCE��DB���ڵ�F��
��1����֤��BF��BC��
��2����AB��4cm��AD��3cm����CF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������龳��
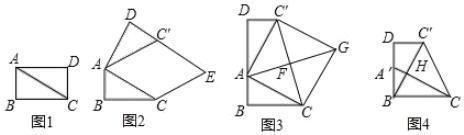
���ۺ���ʵ�����ϣ���ʦ��ͬѧ���ԡ�����ֽƬ�ļ�ƴ��Ϊ���չ��ѧ����� ͼ 1����������ֽƬ ABCD �ضԽ��� AC �������õ���ABC �͡�ACD���������� AB ��4cm��AC��8cm��
�������֣�
��1����ͼ 1 �еġ�ACD �Ե� A Ϊ��ת���ģ�����ʱ�뷽����ת�Ϧ���ʹ�Ϧ�����BAC���õ���ͼ 2 ��ʾ�ġ�AC��D������ C �� AC���ƽ���ߣ��� DC'���ӳ��� ���ڵ� E�����ı��� ACEC�����״�� ��
��2������С�齫ͼ 1 �еġ�ACD �Ե� A Ϊ��ת���ģ�����ʱ�뷽����ת��ʹ B�� A��D ������ͬһ��ֱ���ϣ��õ���ͼ 3 ��ʾ�ġ�AC��D������ CC'��ȡ CC����� �� F������ AF ���ӳ����� G��ʹ FG��AF������ CG��C��G���õ��ı��� ACGC�䣬 �������������Σ�����֤��������ۣ�
ʵ��̽����
��3������С���ڴ���С�鷢�ֽ��۵Ļ����ϣ��������²���������ABC ���� BD ����ƽ�ƣ�ʹ�� B ��� A �غϣ���ʱ A ��ƽ���� A'�㣬A'C �� BC���ཻ�ڵ� H�� ��ͼ 4 ��ʾ������ CC�䣬���� tan��C��CH ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() �ӵ�
�ӵ�![]() ������
������![]() ������ÿ��2����λ���ȵ��ٶ����
������ÿ��2����λ���ȵ��ٶ����![]() �����˶���ͬʱ��
�����˶���ͬʱ��![]() �ӵ�
�ӵ�![]() ������
������![]() ������ÿ��1����λ���ȵ��ٶ����
������ÿ��1����λ���ȵ��ٶ����![]() �����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������
�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������![]() �˶���ʱ����
�˶���ʱ����![]() ��
��![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��
��1��![]() ______�����ú�
______�����ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
��2���ı���![]() �ܹ���Ϊ����������ܣ������Ӧ��
�ܹ���Ϊ����������ܣ������Ӧ��![]() ֵ��������ܣ���˵�����ɣ�
ֵ��������ܣ���˵�����ɣ�
��3����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() Ϊֱ�������Σ���˵�����ɣ�
Ϊֱ�������Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����У�ֻ�������Խ��Խ�ܵ����Ĺ�ע�������١��ڼ䣬ijУС�������������ij����������ѧ���ͼҳ�����ѧ�����ֻ�����Ŀ�����ͳ�����������������µ�ͳ��ͼ��

��1������ε���ļҳ�����������ȫͼ1��
��2����ͼ2�б�ʾ�ҳ����ɡ���Բ�ĽǵĶ�����
��3����֪ij������6500���ҳ����������з�����ѧ�����ֻ��Ĵ�Լ�ж������ҳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
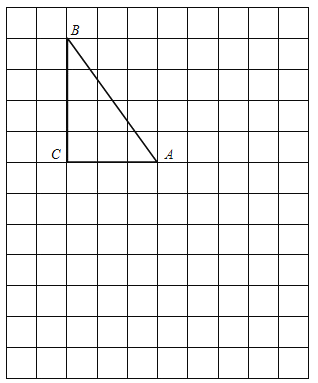
����Ŀ������ͼ����ͼ�У�ÿ��С�����εı߳���Ϊ1����λ����Rt��ABC�У���C��90����AC��3��BC��4��
��1������ͼ��������ABC��AΪ��ת���ģ���˳ʱ�뷽����ת90�����ͼ�Ρ�AB1C1��
��2������B������Ϊ����3��5��������ͼ�л���ֱ������ϵ����ֱ��д��A��C��������ꣻ
��3�����ݣ�2��������ϵ�������ABC����ԭ��ԳƵ�ͼ�Ρ�A2B2C2����ֱ��д����A2��B2��C2�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳��ƻ�����A��B�����ͺŵ��ֻ�����֪ÿ��A�ͺ��ֻ��Ľ��۱�ÿ��B�ͺ��ֻ����۶�500Ԫ��ÿ��A�ͺ��ֻ����ۼ���2500Ԫ��ÿ��B�ͺ��ֻ����ۼ���2100Ԫ��
��1�����̳���50000Ԫ������A�ͺ��ֻ�10����B�ͺ��ֻ�20������A��B�����ͺŵ��ֻ�ÿ�����۸��Ƕ���Ԫ��
��2��Ϊ�������г������̳������ò�����7.5��Ԫ�ɹ�A��B�����ͺŵ��ֻ���40������A�ͺ��ֻ�������������B�ͺ��ֻ�������2����
�ٸ��̳����ļ��ֽ�����ʽ��
�ڸ��̳�ѡ�����ֽ�����ʽ����õ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
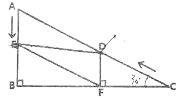
����Ŀ������ѧ����ϣ���ʦ�����һ�����⣺��һ�����dz���ͼ�ڷţ�ֱ�����dzߵ�����ֱ�DZ߷ֱ�ֱ��ƽ�У�60���ǵĶ�������һ�����dzߵ�б�����ƶ���������˶������У�����Щ���������о�����֮��Ĺ�ϵ��
С��ѡ��������һ�Ա���������ѧϰ�����ľ��飬������֮��Ĺ�ϵ������̽����
������С�ֵ�̽�����̣��벹��������
��1����������ͼ�Σ���ȷ������̽������
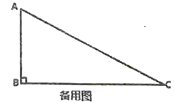
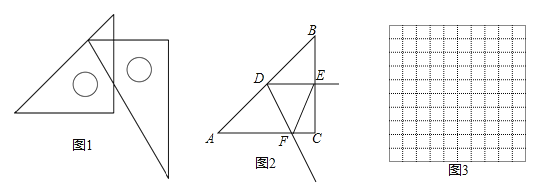
��ͼ2����Rt��ABC�У���C=90����AC=BC=6cm��D���߶�AB��һ���㣬����DE��BC�ڵ�E����EDF=60��������DF������AC���ڵ�F����B��E�����ľ���Ϊxcm��E��F�����ľ���Ϊycm��
��2��ͨ��ȡ�㡢��ͼ���������õ���x��y�ļ���ֵ�����±���
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 6.9 | 5.3 | 4.0 | 3.3 | 4.5 | 6 |
��˵������ȫ����ʱ������ݱ���һλС����
��3������ƽ��ֱ������ϵ������Բ�ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ��
��4����ϻ����ĺ���ͼ������⣺����DEFΪ�ȱ�������ʱ��BE�ij���ԼΪ cm��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com