
分析 (1)总利润=每个的利润×销售量,销售量为(400-10x)个,列方程求解,根据题意取舍;
(2)利用函数的性质求最值.
解答 解:(1)设每个定价增加x元.
列出方程为:(x+10)(400-10x)=6000,
解得:x1=10,x2=20,
要使进货量较少,则每个定价为50+20=70元,应进货400-10x=400-10×20200个.
答:每个定价为70元,应进货200个.
(2)设每个定价增加x元,获得利润为y元.
y=(x+10)(400-10x)=-10x2+300x+4000=-10(x-15)2+6250,
当x=15时,y有最大值为6250.
所以每个定价为65元时得最大利润,可获得的最大利润是6250元.
点评 本题主要考查的是二次函数的应用、一元二次方程的应用,明确总利润=每个的利润×销售量是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
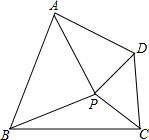 P为四边形ABCD内一点,如果△PAB和△PCD都是以AB,CD为底的等腰直角三角形,则该四边形称为“对底四边形”,AB,CD叫底.
P为四边形ABCD内一点,如果△PAB和△PCD都是以AB,CD为底的等腰直角三角形,则该四边形称为“对底四边形”,AB,CD叫底.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
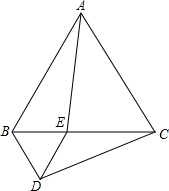 如图,等边三角形ABC的边长为4,点E是边BC上一动点(不与点B、C重合),以BE为边在BC的下方作等边三角形BDE,连接AE、CD.
如图,等边三角形ABC的边长为4,点E是边BC上一动点(不与点B、C重合),以BE为边在BC的下方作等边三角形BDE,连接AE、CD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com