
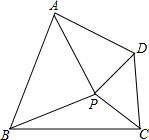
 P为四边形ABCD内一点,如果△PAB和△PCD都是以AB,CD为底的等腰直角三角形,则该四边形称为“对底四边形”,AB,CD叫底.
P为四边形ABCD内一点,如果△PAB和△PCD都是以AB,CD为底的等腰直角三角形,则该四边形称为“对底四边形”,AB,CD叫底.分析 (1)连接AC、BD,如图1,由△PAB和△PCD都是等腰直角三角形,可证得△BPD≌△APC,根据全等三角形的性质可得AC=BD,∠PBD=∠PAC,从而可得∠AOB=∠APB=90°,然后运用勾股定理就可证得AB2+CD2=AD2+BC2.过点C作CF⊥BP,交BP的延长线于F,过点D作DE⊥AP于E,如图2,不妨设AB=m,CD=n,∠APD=α,根据同角的余角相等可得∠FPC=∠APD=α,然后运用三角函数表示出△APD和△BPC的高,就可得到△APD和△BPC的面积相等;
(2)利用(1)中的结论,可得S=$\frac{1}{4}$m2+$\frac{1}{4}$n2+$\frac{1}{2}$mnsinα,然后借助于sinα的取值范围,就可得到S的范围.
解答 解:(1)连接AC、BD,如图1,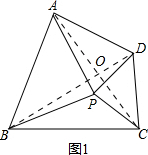
∵△PAB和△PCD都是以AB,CD为底的等腰直角三角形,
∴PA=PB,PC=PD,∠APB=∠CPD=90°,
∴∠BPD=∠APC.
在△BPD和△APC中,
$\left\{\begin{array}{l}{PB=PA}\\{∠BPD=∠APC}\\{PD=PC}\end{array}\right.$,
∴△BPD≌△APC,
∴AC=BD,∠PBD=∠PAC,
∴∠AOB=∠APB=90°,
∴AC⊥BD,
∴AB2=AO2+BO2,DC2=DO2+OC2,AD2=OA2+OD2,BC2=OB2+OC2,
∴AB2+CD2=AD2+BC2.
过点C作CF⊥BP,交BP的延长线于F,过点D作DE⊥AP于E,如图2,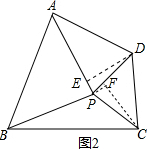
不妨设AB=m,CD=n,∠APD=α,
则有∠FPC=90°-∠DPF=∠APD=α,
∴DE=DPsinα=$\frac{\sqrt{2}}{2}$nsinα,CF=CPsinα=$\frac{\sqrt{2}}{2}$nsinα,
∴S△APD=$\frac{1}{2}$AP•DE=$\frac{1}{2}$•$\frac{\sqrt{2}}{2}$m•$\frac{\sqrt{2}}{2}$nsinα=$\frac{1}{4}$mnsinα,
S△BPC=$\frac{1}{2}$BP•CF=$\frac{1}{2}$•$\frac{\sqrt{2}}{2}$m•$\frac{\sqrt{2}}{2}$nsinα=$\frac{1}{4}$mnsinα,
∴S△APD=S△BPC.
综上所述:①②③④正确.
故答案为①②③④;
(2)S=S△ABP+S△CPD+S△APD+S△BPC
=$\frac{1}{2}$m•$\frac{1}{2}$m+$\frac{1}{2}$n•$\frac{1}{2}$n+$\frac{1}{4}$mnsinα+$\frac{1}{4}$mnsinα
=$\frac{1}{4}$m2+$\frac{1}{4}$n2+$\frac{1}{2}$mnsinα.
∵0<sinα≤1,
∴$\frac{1}{4}$m2+$\frac{1}{4}$n2<S≤$\frac{1}{4}$m2+$\frac{1}{4}$n2+$\frac{1}{2}$mn.
故答案为$\frac{1}{4}$m2+$\frac{1}{4}$n2<S≤$\frac{1}{4}$m2+$\frac{1}{4}$n2+$\frac{1}{2}$mn.
点评 本题主要考查了等腰直角三角形的性质、全等三角形的判定与性质、勾股定理、锐角三角函数、三角函数值的范围等知识,运用0<sinα≤1是解决第2小题的关键.


科目:初中数学 来源: 题型:解答题
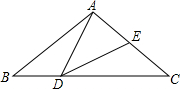 如图,在△ABC中,AB=AC=2,点D在线段BC上运动(点D不与B、C重合),∠B=40°,连结AD,作∠ADE=40°,DE交线段AC于E.
如图,在△ABC中,AB=AC=2,点D在线段BC上运动(点D不与B、C重合),∠B=40°,连结AD,作∠ADE=40°,DE交线段AC于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
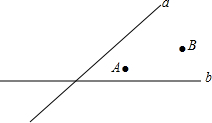 李明准备与朋友经营一个超市,经调查发现他家附近有两个大的居民区A、B,同时又有相交的两条公路a、b(如图所示),李明想把超市建在到两居民区的距离,到两公路的距离分别相等的位置上,请用尺规作图确定超市P的位置.(作图不写作法,但要求保留作图痕迹)
李明准备与朋友经营一个超市,经调查发现他家附近有两个大的居民区A、B,同时又有相交的两条公路a、b(如图所示),李明想把超市建在到两居民区的距离,到两公路的距离分别相等的位置上,请用尺规作图确定超市P的位置.(作图不写作法,但要求保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
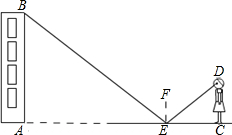 小玲用下面的方法来测量学校教学大楼AB的高度:如图,在水平地面上放一面平面镜,镜子与教学大楼的距离EA=25米.当她与镜子的距离CE=2.5米时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.6米.请你帮助小玲计算出教学大楼的高度AB是多少米(注意:根据光的反射定律:反射角等于入射角).
小玲用下面的方法来测量学校教学大楼AB的高度:如图,在水平地面上放一面平面镜,镜子与教学大楼的距离EA=25米.当她与镜子的距离CE=2.5米时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.6米.请你帮助小玲计算出教学大楼的高度AB是多少米(注意:根据光的反射定律:反射角等于入射角).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
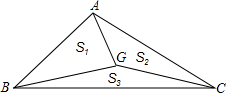 如图,G是△ABC的重心,其中△ABG、△ACG、△BCG的面积分别表示为S1、S2、S3,那么有( )
如图,G是△ABC的重心,其中△ABG、△ACG、△BCG的面积分别表示为S1、S2、S3,那么有( )| A. | S1=S2=S3 | B. | S1<S2<S3 | C. | S1=S2<S3 | D. | S1=S2>S3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间x(天) | 1≤x≤40 | 40≤x≤70 |
| 售价(元/件) | x+45 | 85 |
| 每天销售(件) | 150-2x | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com