Question

如图1，AB是圆O的直径，点C在AB的延长线上，AB=4，BC=2，P是圆O上半部分的一个动点，连接OP，CP．

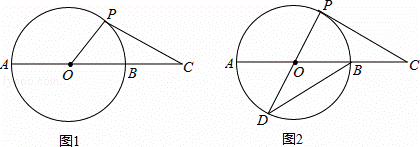
（1）求△OPC的最大面积；

（2）求∠OCP的最大度数；设∠OCP=α，当线段CP与圆O只有一个公共点（即P点）时，求α的范围（直接写出答案）；

（3）如图2，延长PO交圆O于点D，连接DB，当CP=DB，求证：CP是圆O的切线．

Answer 1

（1）解：∵AB=4，

∴OB=2，OC=OB+BC=4．

在△OPC中，设OC边上的高为h，

∵S_△OPC=OC•h=2h，

∴当h最大时，S_△OPC取得最大值．

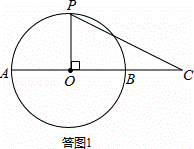
观察图形，当OP⊥OC时，h最大，如答图1所示：

此时h=半径=2，S_△OPC=2×2=4．

∴△OPC的最大面积为4．

（2）解：当PC与⊙O相切时，∠OCP最大．如答图2所示：

∵sin∠OCP===，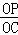

∴∠OCP=30°

∴∠OCP的最大度数为30°．

∴设∠OCP=α，当线段CP与圆O只有一个公共点（即P点）时，0＜α≤30°；

（3）证明：图3，连接AP，BP．

∴∠A=∠D=∠APD=∠ABD，

∵=，

∴=，

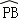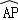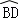∴AP=BD，

∵CP=DB，

∴AP=CP，

∴∠A=∠C

∴∠A=∠D=∠APD=∠ABD=∠C，

在△ODB与△BPC中，

，

∴△ODB≌△BPC（SAS），

∴∠D=∠BPC，

∵PD是直径，

∴∠DBP=90°，

∴∠D+∠BPD=90°，

∴∠BPC+∠BPD=90°，

∴DP⊥PC，

∵DP经过圆心，

∴PC是⊙O的切线．