
分析 先从第1个式子入手,分子都是1,主要看分母,第一个数的分母依次是1、3、5、…,是连续奇数,第2个分数的分母是2、4、6等是连续偶数,比第1个分母大1,第3个分数的分母与式子的个数相同,由此可得出第n个式子,同时就可以写出其他结论.
解答 解:第1个式子:$\frac{1}{1}$+$\frac{1}{2}$-1=$\frac{1}{2}$,
第2个式子:$\frac{1}{3}$+$\frac{1}{4}$-$\frac{1}{2}$=$\frac{1}{12}$,
第3个式子:$\frac{1}{5}$+$\frac{1}{6}$-$\frac{1}{3}$=$\frac{1}{30}$,
第4个式子:$\frac{1}{7}$+$\frac{1}{8}$-$\frac{1}{4}$=$\frac{1}{56}$,
2012÷2=1006,
第1006个式子:$\frac{1}{2×1006-1}$+$\frac{1}{2×1006}$-$\frac{1}{1006}$=$\frac{1}{2011}$+$\frac{1}{2012}$-$\frac{1}{1006}$=$\frac{1}{2011×2012}$,
第n个式子:$\frac{1}{2n-1}$+$\frac{1}{2n}$-$\frac{1}{n}$=$\frac{1}{2n-1}$+$\frac{1-2}{2n}$=$\frac{1}{2n-1}$-$\frac{1}{2n}$=$\frac{2n-(2n-1)}{2n(2n-1)}$=$\frac{1}{2n(2n-1)}$,
故答案为:$\frac{1}{1006}$,$\frac{1}{2n-1}$+$\frac{1}{2n}$-$\frac{1}{n}$=$\frac{1}{2n(2n-1)}$.
点评 本题考查了数字类的规律题,此类题形式多样,它要求在已有知识的基础上去探究,观察思考并发现规律,一般情况下要从第1个式子进行分析,从而得出结论.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:解答题
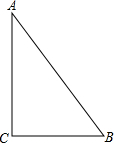 如图,要在一块形状为直角三角形(∠C 为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮画出一个半圆,使它的圆心在线段AC 上,且与AB、BC 都相切.
如图,要在一块形状为直角三角形(∠C 为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮画出一个半圆,使它的圆心在线段AC 上,且与AB、BC 都相切.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
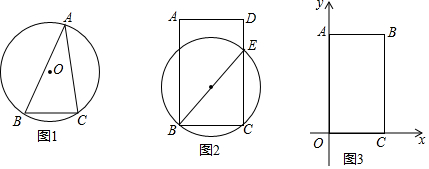
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
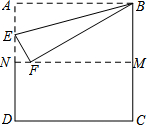 把正方形ABCD沿对边中点所在直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE,若AB的长为2,则FM=$\sqrt{3}$.
把正方形ABCD沿对边中点所在直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE,若AB的长为2,则FM=$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
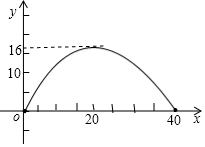 如图建立直角坐标系,某抛物线型桥拱的最大高度为16米,跨度为40米,则它对应的解析式为:y=-$\frac{1}{25}$x2+$\frac{2}{5}$x.
如图建立直角坐标系,某抛物线型桥拱的最大高度为16米,跨度为40米,则它对应的解析式为:y=-$\frac{1}{25}$x2+$\frac{2}{5}$x.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在等腰Rt△ABC中,AC=BC=2$\sqrt{2}$,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是π.
如图,在等腰Rt△ABC中,AC=BC=2$\sqrt{2}$,点P在以斜边AB为直径的半圆上,M为PC的中点.当点P沿半圆从点A运动至点B时,点M运动的路径长是π.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知点B.C.D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H.
如图,已知点B.C.D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com