
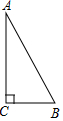
 如图,在△ABC中,∠C=90°,AB=10cm,BC=6cm,两只小虫(不计大小)分别从C点出发,小虫1沿CA-AB-BC运动,速度大小为2cm/s,小虫2沿CB-BA-AC运动,速度大小为$\frac{3}{2}$cm/s,相遇后停止.这一过程中两小虫之间的距离y与时间t的关系的大致图象是( )
如图,在△ABC中,∠C=90°,AB=10cm,BC=6cm,两只小虫(不计大小)分别从C点出发,小虫1沿CA-AB-BC运动,速度大小为2cm/s,小虫2沿CB-BA-AC运动,速度大小为$\frac{3}{2}$cm/s,相遇后停止.这一过程中两小虫之间的距离y与时间t的关系的大致图象是( )| A. | 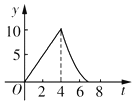 | B. | 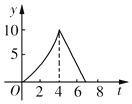 | C. | 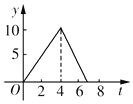 | D. | 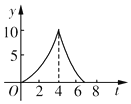 |
 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
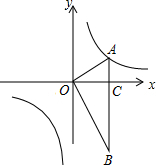 如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A($\sqrt{3}$,1)在反比例函数y=$\frac{k}{x}$(x≠0)的图象上.
如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A($\sqrt{3}$,1)在反比例函数y=$\frac{k}{x}$(x≠0)的图象上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
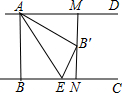 如图,已知AD∥BC,AB⊥BC,AB=3,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M、N,当点MB′=$\frac{1}{3}$MN时,BE的长为$\frac{3\sqrt{2}}{2}$.
如图,已知AD∥BC,AB⊥BC,AB=3,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M、N,当点MB′=$\frac{1}{3}$MN时,BE的长为$\frac{3\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
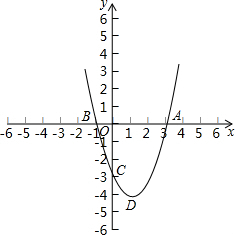 如图,在平面直角坐标系中,二次函数y=x2+bx+c的对称轴为经过点(1,0)的直线,其图象与x轴交于点A、B,且过点C(0,-3),其顶点为D.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的对称轴为经过点(1,0)的直线,其图象与x轴交于点A、B,且过点C(0,-3),其顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
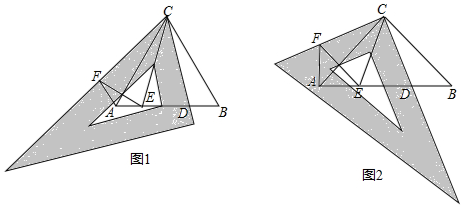
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
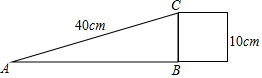 为了方便行人推车过某天桥,市政府在10m高的天桥一侧修建了40m长的斜道(如图所示),我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是( )
为了方便行人推车过某天桥,市政府在10m高的天桥一侧修建了40m长的斜道(如图所示),我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是( )| A. |  | B. |  | ||
| C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
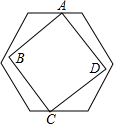 如图,有一个边长不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组平行的对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是$\frac{\sqrt{6}}{2}$≤a≤3-$\sqrt{3}$.
如图,有一个边长不定的正方形ABCD,它的两个相对的顶点A,C分别在边长为1的正六边形一组平行的对边上,另外两个顶点B,D在正六边形内部(包括边界),则正方形边长a的取值范围是$\frac{\sqrt{6}}{2}$≤a≤3-$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com