
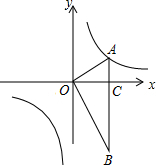
 如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A($\sqrt{3}$,1)在反比例函数y=$\frac{k}{x}$(x≠0)的图象上.
如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A($\sqrt{3}$,1)在反比例函数y=$\frac{k}{x}$(x≠0)的图象上.分析 (1)将点A($\sqrt{3}$,1)代入y=$\frac{k}{x}$,利用待定系数法即可求出反比例函数的表达式;
(2)先解△OAB,得出∠ABO=30°,再根据旋转的性质求出E点坐标为(-$\sqrt{3}$,-1),即可求解.
解答 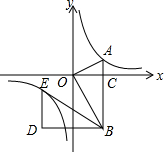 解:(1)∵点A( $\sqrt{3}$,1)在反比例函数 y=$\frac{k}{x}$的图象上,
解:(1)∵点A( $\sqrt{3}$,1)在反比例函数 y=$\frac{k}{x}$的图象上,
∴k=$\sqrt{3}$×1=$\sqrt{3}$.
∵A( $\sqrt{3}$,1),
∴OA=2,
由OA⊥OB,AB⊥x轴,易证△OC∽△ABO,
∴$\frac{AO}{AB}$=$\frac{AC}{AO}$,即 $\frac{2}{AB}$=$\frac{1}{2}$,
∴AB=4,
∴B($\sqrt{3}$,-3);
(2)∵OB=$\sqrt{{4}^{2}-(\sqrt{3})^{2}}$=2 $\sqrt{3}$,
∴sin∠ABO=$\frac{OA}{AB}$=$\frac{1}{2}$,
∴∠ABO=30°.
∵将△BOA绕点B按逆时针方向旋转60°得到△BDE,
∴△BOA≌△BDE,∠OBD=60°,
∴BO=BD=2 $\sqrt{3}$,OA=DE=2,∠BOA=∠BDE=90°,
∠ABD=30°+60°=90°.
又BD-OC=2 $\sqrt{3}$-$\sqrt{3}$=$\sqrt{3}$,BC-DE=4-1-2=1,
∴E(-$\sqrt{3}$,-1),
∵-$\sqrt{3}$×(-1)=$\sqrt{3}$,
∴点E在该反比例函数的图象上.
点评 本题考查了待定系数法求反比例函数的解析式,反比例函数图象上点的坐标特征,旋转的性质,正确求出解析式是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
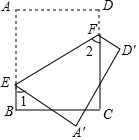 如图,E、F分别是矩形ABCD边AB、CD上的点,将矩形ABCD沿EF折叠,使A、D分别落在A′和D′处,若∠1=50°,则∠2的度数是( )
如图,E、F分别是矩形ABCD边AB、CD上的点,将矩形ABCD沿EF折叠,使A、D分别落在A′和D′处,若∠1=50°,则∠2的度数是( )| A. | 65° | B. | 60° | C. | 50° | D. | 40° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 128元 | B. | 130元 | C. | 150元 | D. | 160元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 快件到达地 | 首重现付资费(1kg) | 续重现付资费(每kg) |
| 江西 | 10 | 2 |
| 浙江、上海、广东等 | 12 | 4 |
| 北京、天津、山东等 | 15 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
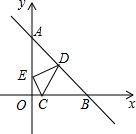 如图,已知点C(1,0),直线y=-x+7与两坐标轴分别交于A、B两点,D、E分别是AB,OA上的动点,当△CDE周长最小时,点D坐标为($\frac{25}{7}$,$\frac{24}{7}$).
如图,已知点C(1,0),直线y=-x+7与两坐标轴分别交于A、B两点,D、E分别是AB,OA上的动点,当△CDE周长最小时,点D坐标为($\frac{25}{7}$,$\frac{24}{7}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
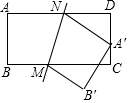 如图,矩形纸片ABCD中,AB=1,BC=2,点M,N分别在边BC,AD上,将纸片ABCD沿直线MN对折,使点A落在CD边上,则线段BM的取值范围是$\frac{3}{4}$≤BM≤1.
如图,矩形纸片ABCD中,AB=1,BC=2,点M,N分别在边BC,AD上,将纸片ABCD沿直线MN对折,使点A落在CD边上,则线段BM的取值范围是$\frac{3}{4}$≤BM≤1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
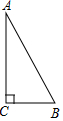 如图,在△ABC中,∠C=90°,AB=10cm,BC=6cm,两只小虫(不计大小)分别从C点出发,小虫1沿CA-AB-BC运动,速度大小为2cm/s,小虫2沿CB-BA-AC运动,速度大小为$\frac{3}{2}$cm/s,相遇后停止.这一过程中两小虫之间的距离y与时间t的关系的大致图象是( )
如图,在△ABC中,∠C=90°,AB=10cm,BC=6cm,两只小虫(不计大小)分别从C点出发,小虫1沿CA-AB-BC运动,速度大小为2cm/s,小虫2沿CB-BA-AC运动,速度大小为$\frac{3}{2}$cm/s,相遇后停止.这一过程中两小虫之间的距离y与时间t的关系的大致图象是( )| A. | 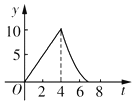 | B. | 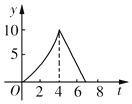 | C. | 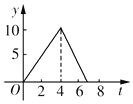 | D. | 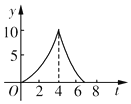 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com