
【题目】已知四边形![]() 为
为![]() 的内接四边形,直径
的内接四边形,直径![]() 与对角线
与对角线![]() 相交于点
相交于点![]() ,作
,作![]() 于
于![]() ,
,![]() 与过
与过![]() 点的直线相交于点
点的直线相交于点![]() ,
,![]() .
.
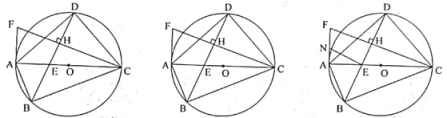
(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)若![]() 平分
平分![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,![]() 为
为![]() 的中点,连接
的中点,连接![]() ,若
,若![]() ,
,![]() 的半径为
的半径为![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析(2)证明见解析(3)![]()
【解析】
(1)根据直径所对的圆周角为90°,得到∠ADC=90°,根据直角三角形两锐角互余得到∠DAC+∠DCA=90°,再根据同弧或等弧所对的圆周角相等,可得到∠FAD+∠DAC=90°,即可得出结论;
(2)连接OD.根据圆周角定理和角平分线定义可得∠DOA=∠DOC,即可得出结论;
(3)连接OD交CF于M,作EP⊥AD于P.可求出AD=4,AF∥OM.根据三角形中位线定理得出OM=![]() AF.证明△ODE≌△OCM,得到OE=OM.设OM=m,用m表示出OE,AE,AP,DP.通过证明△EAN∽△DPE,根据相似三角形对应边成比例,求出m的值,从而求得AN,AE的值.在Rt△NAE中,由勾股定理即可得出结论.
AF.证明△ODE≌△OCM,得到OE=OM.设OM=m,用m表示出OE,AE,AP,DP.通过证明△EAN∽△DPE,根据相似三角形对应边成比例,求出m的值,从而求得AN,AE的值.在Rt△NAE中,由勾股定理即可得出结论.
(1)∵AC为⊙O的直径,
∴∠ADC=90°,
∴∠DAC+∠DCA=90°.
∵![]() ,
,
∴∠ABD=∠DCA.
∵∠FAD=∠ABD,
∴∠FAD=∠DCA,
∴∠FAD+∠DAC=90°,
∴CA⊥AF,
∴AF为⊙O的切线.

(2)连接OD.
∵![]() ,
,
∴∠ABD=![]() ∠AOD.
∠AOD.
∵![]() ,
,
∴∠DBC=![]() ∠DOC.
∠DOC.
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠DOA=∠DOC,
∴DA=DC.
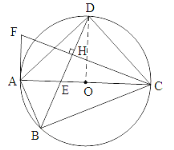
(3)连接OD交CF于M,作EP⊥AD于P.
∵AC为⊙O的直径,
∴∠ADC=90°.
∵DA=DC,
∴DO⊥AC,
∴∠FAC=∠DOC=90°,AD=DC=![]() =4,
=4,
∴∠DAC=∠DCA=45°,AF∥OM.
∵AO=OC,
∴OM=![]() AF.
AF.
∵∠ODE+∠DEO=90°,∠OCM+∠DEO=90°,
∴∠ODE=∠OCM.
∵∠DOE=∠COM,OD=OC,
∴△ODE≌△OCM,
∴OE=OM.
设OM=m,
∴OE=m,![]() ,
,![]() ,
,
∴![]() .
.
∵∠AED+∠AEN=135°,∠AED+∠ADE=135°,
∴∠AEN=∠ADE.
∵∠EAN=∠DPE,
∴△EAN∽△DPE,
∴![]() ,
,
∴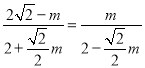 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
由勾股定理得:![]() .
.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】如图,半圆D的直径AB=4,线段OA=7,O为原点,点B在数轴的正半轴上运动,点B在数轴上所表示的数为m.
(1)当半圆D与数轴相切时,m= .
(2)半圆D与数轴有两个公共点,设另一个公共点是C.
①直接写出m的取值范围是 .
②当BC=2时,求△AOB与半圆D的公共部分的面积.
(3)当△AOB的内心、外心与某一个顶点在同一条直线上时,求tan∠AOB的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
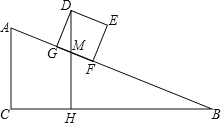
【题目】某仓储中心有一个坡度为i=1:2的斜坡AB,顶部A处的高AC为4米,B、C在同一水平地面上,其横截面如图.
(1)求该斜坡的坡面AB的长度;
(2)现有一个侧面图为矩形DEFG的长方体货柜,其中长DE=2.5米,高EF=2米,该货柜沿斜坡向下时,点D离BC所在水平面的高度不断变化,求当BF=3.5米时,点D离BC所在水平面的高度DH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查.调查结果显示,支付方式有:A微信、B支付宝、C现金、D其他,该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.

请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了多少名购买者?
(2)请补全条形统计图;在扇形统计图中A种支付方式所对应的圆心角为 度.
(3)若该超市这一周内有1600名购买者,请你估计使用A和B两种支付方式的购买者共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
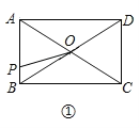
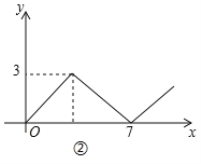
【题目】如图①,在矩形![]() 中,
中,![]() ,对角线
,对角线![]() 相交于点
相交于点![]() ,动点
,动点![]() 由点
由点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动.设点
运动.设点![]() 的运动路程为
的运动路程为![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() 与
与![]() 的函数关系图象如图②所示,则
的函数关系图象如图②所示,则![]() 边的长为( ).
边的长为( ).
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知P(-5,m)和Q(3,m)是二次函数y=2x2+bx+1图象上的两点.
(1)求b的值;
(2)将二次函数y=2x2+bx+1的图象进行一次平移,使图象经过原点.(写出一种即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
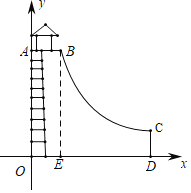
【题目】如图所示的是太原市某公园“水上滑梯”的侧面图,其中![]() 段可看成是双曲线的一部分,其中,矩形
段可看成是双曲线的一部分,其中,矩形![]() 中有一个向上攀爬的梯子,
中有一个向上攀爬的梯子,![]() 米,入口
米,入口![]() ,且
,且![]() 米,出口
米,出口![]() 点距水面的距离
点距水面的距离![]() 为
为![]() 米,则点
米,则点![]() 之间的水平距离
之间的水平距离![]() 的长度为( )
的长度为( )
A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com