
【题目】如图,![]() 中,AB=9cm,AC=6cm,两内角平分线BO和CO相交于点O.
中,AB=9cm,AC=6cm,两内角平分线BO和CO相交于点O.

(1)若∠A=70,求∠BOC的度数.
(2)若直线DE过点O,与AB、AC分别相交于点D、E,且DE//BC,求![]() 的周长.
的周长.
【答案】(1)![]() ;(2)15cm
;(2)15cm
【解析】
(1)根据三角形的内角和定理求出∠ABC+∠ACB,再根据角平分线的定义求出∠OBC+∠OCB,然后利用三角形的内角和定理列式计算即可得解.
(2)根据平行线的性质和角平分线的性质,得到∠DBO=∠DOB,则BD=OD,同理可得OE=EC,即可求出三角形的周长.
解:(1)在△ABC中,∠ABC+∠ACB=180°![]() ∠A=180°
∠A=180°![]() 70°=110°,
70°=110°,
∵∠ABC与∠ACB的角平分线BO,CO相交于点O,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() ×110°=55°,
×110°=55°,
在△BOC中,∠BOC=180°![]() (∠OBC+∠OCB)=180°
(∠OBC+∠OCB)=180°![]() 55°=125°.
55°=125°.
(2)如图:
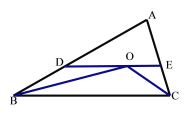
∵DE∥BC,
∴∠DOB=∠OBC,
又∵BO是∠ABC的角平分线,
∴∠DBO=∠OBC,
∴∠DBO=∠DOB,
∴BD=OD,
同理:OE=EC,
∴△ADE的周长=AD+OD+OE+AE=AD+BD+AE+EC=AB+AC=15cm.


 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:
【题目】如图,正五边形ABCDE内接于⊙O,过点A作⊙O的切线交对角线DB的延长线于点F,则下列结论不成立的是( )
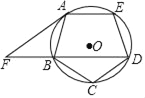
A. AE∥BD B. AB=BF C. AF∥CD D. DF=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
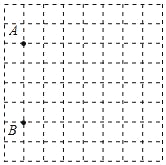
【题目】十一期间,小明一家一起去旅游,如图是小明设计的某旅游景点的图纸(网格是由相同的小正方形组成的,且小正方形的边长代表实际长度100m,在该图纸上可看到两个标志性景点A,B.若建立适当的平面直角坐标系,则点A(﹣3,1),B(﹣3,﹣3),第三个景点C(1,3)的位置已破损.
(1)请在图中画出平面直角坐标系,并标出景点C的位置;
(2)平面直角坐标系的坐标原点为点O,△ACO是直角三角形吗?请判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:

(1)如图①,已知:![]() .求作:射线
.求作:射线![]() ,使
,使![]() 平分
平分![]() .(要求:尺规作图,不写作法,但需保留作图痕迹) .
.(要求:尺规作图,不写作法,但需保留作图痕迹) .
(2)题(1)中作图的依据是全等三角形判定方法中的__________.
(3)在图②中作出![]() ,使它与
,使它与![]() 关于
关于![]() 轴对称.
轴对称.
(4)在图②中的![]() 轴上找到一点
轴上找到一点![]() ,使
,使![]() 的周长最小.
的周长最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点O为坐标原点,点A、B、C的坐标分别为A(![]() ,0)、B(3
,0)、B(3![]() ,0)、C(0,5),点D在第一象限内,且∠ADB=60°,则线段CD的长的最小值是( )
,0)、C(0,5),点D在第一象限内,且∠ADB=60°,则线段CD的长的最小值是( )
A. 2![]() ﹣2 B. 2
﹣2 B. 2![]() C. 2
C. 2![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商场销售一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下.若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
(2)每千克水果涨价多少元时,商场每天获得的利润最大?获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴交于点M.

(1)求此抛物线的解析式和对称轴;
(2)在此抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com