
【题目】(10分)如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴交于点M.

(1)求此抛物线的解析式和对称轴;
(2)在此抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
【答案】(1)y=![]() ,抛物线的对称轴是 x=3;
,抛物线的对称轴是 x=3;
(2)存在;P点坐标为(3,![]() ).
).
(3)在直线AC下方的抛物线上存在点N,使△NAC面积最大.N(![]() ,-3)
,-3)
【解析】
(1)根据已知条件可设抛物线的解析式为y=a(x-1)(x-5).
把点A(0,4)代入上式,解得a=![]() .
.
∴y=![]() (x-1)(x-5)=
(x-1)(x-5)=![]() x2-
x2-![]() x+4=
x+4=![]() (x-3)2-
(x-3)2-![]() .
.
∴抛物线的对称轴是x=3.
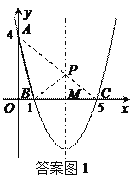
(2)存在,P点的坐标是(3,![]() ).如图1,连接AC交对称轴于点P,连接BP,AB.
).如图1,连接AC交对称轴于点P,连接BP,AB.
∵点B与点C关于对称轴对称,
∴PB=PC.
∴AB+AP+PB=AB+AP+PC=AB+AC.
∴此时△PAB的周长最小.
设直线AC的解析式为y=kx+b.把A(0,4),C(5,0)代入y=kx+b,得
![]() 解得
解得
∴y=-![]() x+4.
x+4.
∵点P的横坐标为3,
∴y=-![]() ×3+4=
×3+4=![]() .
.
∴P(3,![]() ).
).
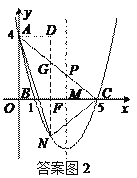
(3)在直线AC下方的抛物线上存在点N,使△NAC的面积最大.
如图2,设N点的横坐标为tt,此时点N(t,![]() t2-
t2-![]() t+4)(0<t<5).
t+4)(0<t<5).
过点N作y轴的平行线,分别交x轴,AC于点F,G,过点A作AD⊥NG,垂足为D.
由(2)可知直线AC的解析式为y=-![]() x+4.
x+4.
把x=t代入y=-![]() x+4,得y=-
x+4,得y=-![]() t+4.
t+4.
∴G(t,-![]() t+4).
t+4).
∴NG=-![]() t+4-(
t+4-(![]() t2-
t2-![]() t+4)=-
t+4)=-![]() t2+4t.
t2+4t.
∵AD+CF=OC=5,
∴S△NAC=S△ANG+S△CGN=![]() NG·AD+
NG·AD+![]() NG·CF=
NG·CF=![]() NG·OC
NG·OC
=![]() ×(-
×(-![]() t2+4t)×5=-2t2+10t=-2(t-
t2+4t)×5=-2t2+10t=-2(t-![]() )2+
)2+![]() .
.
∵当t=![]() 时,△NAC面积的最大值为
时,△NAC面积的最大值为![]() .
.
由t=![]() ,得y=
,得y=![]() ×(
×(![]() )2-
)2-![]() ×
×![]() +4=-3.
+4=-3.
∴N(![]() ,-3).
,-3).


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知点A是射线BE上一点,过A作CA⊥BE交射线BF于点C,AD⊥BF交射线BF于点D,给出下列结论:①∠1是∠B的余角;②图中互余的角共有3对;③∠1的补角只有∠ACF;④与∠ADB互补的角共有3个.则上述结论正确的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC 为等边三角形,点 D、E 分别在边 BC、AC 上,且 AE=CD,AD 与 BE相交于点 F.则∠DFE 的度数为_____°;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆柱,中间是一个圆柱(如图,单位:mm).电镀时,如果每平方米用锌0.11kg,要电镀1000个这样的锚标浮筒需要用多少锌?(精确到1kg)
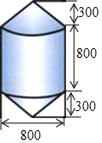
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的是丽水市统计局公布的2010~2013年全社会用电量的折线统计图.

(1)根据统计图填写统计表:
2010~2013年丽水市全社会用电量统计表
年份 | 2010 | 2011 | 2012 | 2013 |
全社会用电量 (单位:亿KW·h) | 13.33 |
(2)根据丽水市2010年至2013年全社会用电量统计数据,求2011~2013年全社会用电量的年平均增长率(保留到0.01).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=(x﹣1)2+k的图象与x轴交于点A(﹣1,0),C两点,与y轴交于点B.
(1)求抛物线解析式及B点坐标;
(2)在抛物线上是否存在点P使S△PAC=![]() S△ABC?若存在,求出P点坐标,若不存在,请说明理由;
S△ABC?若存在,求出P点坐标,若不存在,请说明理由;
(3)在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形,若存在,求出Q点坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个30°的角BAC与角MON,顶点A在射线ON上某处,现保持角MON不动,将角BAC绕点A以每秒15°的速度顺时针旋转,边AB、AC分别与边OM交于点P、Q,当AC∥OM时,交点Q消失旋转结束。设运动时间为t秒(t>0).



(1)当t=2秒时,OP:PQ= ;
(2)在运动的过程中,△APQ能否成为等腰三角形?若能,请利用备用图,直接写出此时的运动时间;
(3)在(2)中判断△OAQ的形状,并选择其中的一个说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com