
【题目】如图,已知抛物线y=(x﹣1)2+k的图象与x轴交于点A(﹣1,0),C两点,与y轴交于点B.
(1)求抛物线解析式及B点坐标;
(2)在抛物线上是否存在点P使S△PAC=![]() S△ABC?若存在,求出P点坐标,若不存在,请说明理由;
S△ABC?若存在,求出P点坐标,若不存在,请说明理由;
(3)在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形,若存在,求出Q点坐标,若不存在,请说明理由.

【答案】(1) y=x2﹣2x﹣3,点B坐标为(0,﹣3);(2)见解析;(3)见解析.
【解析】
(1)把A(-1,0)代入抛物线y=(x﹣1)2+k,求出k即可解决问题.(2)存在.先求出△ABC的面积,再根据已知条件求出点P的纵坐标,利用待定系数法即可解决问题.(3)存在.分三种情形讨①当AQ=AB时,有两种情形a、当![]() 在x轴上方,;b、当
在x轴上方,;b、当![]() 在x轴下方时,利用勾股定理即可解决问题.②当BA=BQ时,此时Q在x轴上,即
在x轴下方时,利用勾股定理即可解决问题.②当BA=BQ时,此时Q在x轴上,即![]() (1,0)③当QA=QB时,点Q在AB的垂直平分线上,求出线段AB的垂直平分线的解析式即可解决问题.
(1,0)③当QA=QB时,点Q在AB的垂直平分线上,求出线段AB的垂直平分线的解析式即可解决问题.
(1)把A(﹣1,0)代入抛物线y=(x﹣1)2+k得,0=4+k,
∴k=﹣4,
∴抛物线解析式为y=(x﹣1)2﹣4,即y=x2﹣2x﹣3,
令x=0,得y=﹣3,
∴点B坐标为(0,﹣3).
(2)存在.如图1中,
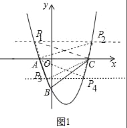
理由:令y=0,则x2﹣2x﹣3=0,
∴x=﹣1或3,
∴点A(﹣1,0),C(3,0),
∴S△ABC=![]() ×4×3=6,
×4×3=6,
∵S△PAC=![]() S△ABC,
S△ABC,
∴S△PAC=![]() ,设P(m,n),
,设P(m,n),
则有![]() ×4×|n|=
×4×|n|=![]() ,
,
∴n=![]() ,
,
当n=![]() 时,m2﹣2m﹣3=
时,m2﹣2m﹣3=![]() ,解得m=﹣
,解得m=﹣![]() 或
或![]() ,此时P(﹣
,此时P(﹣![]() ,
,![]() )或(
)或(![]() ,
,![]() ),
),
当n=﹣![]() 时,m2﹣2m﹣3=﹣
时,m2﹣2m﹣3=﹣![]() ,解得m=
,解得m=![]() 或
或![]() ,此时P(
,此时P(![]() ,﹣
,﹣![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).
综上所述,满足条件的P点坐标为(﹣![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).
(3)如图2中,存在.

①当AQ=AB时,有两种情形a、当Q1在x轴上方,此时Q1(1,![]() );b、当Q2在x轴下方时,此时Q2(1,﹣
);b、当Q2在x轴下方时,此时Q2(1,﹣![]() ).
).
②当BA=BQ时,此时Q在x轴上,Q3(1,0).
③当QA=QB时,点Q在AB的垂直平分线上,
∵A(﹣1,0),B(0,﹣3),
∴直线AB解析式为y=﹣3x﹣3,线段AB的中点为(﹣![]() ,﹣
,﹣![]() ),
),
设线段AB的中垂线的解析式为y=![]() x+m.
x+m.
∴﹣![]() =﹣
=﹣![]() +m,
+m,
∴m=﹣![]() ,
,
∴线段AB的中垂线的解析式为y=![]() x﹣
x﹣![]() ,与对称轴的交点Q4(1,﹣1),
,与对称轴的交点Q4(1,﹣1),
综上所述,满足条件的点Q坐标为(1,![]() )或(1,﹣
)或(1,﹣![]() )或(1,0)或(1,﹣1).
)或(1,0)或(1,﹣1).


科目:初中数学 来源: 题型:
【题目】为了某校七年级学生对![]() 《最强大脑》、
《最强大脑》、![]() 《朗读者》、
《朗读者》、![]() 《中国诗词大会》、
《中国诗词大会》、![]() 《极限挑战》四个电视节目的喜爱情况,随机抽取了
《极限挑战》四个电视节目的喜爱情况,随机抽取了![]() 位学生进行调查统计(要求每位学生选出并且只能选一个自己最喜爱的节目),并将调查结果绘制成如下两幅不完整的统计图(图1,图2)
位学生进行调查统计(要求每位学生选出并且只能选一个自己最喜爱的节目),并将调查结果绘制成如下两幅不完整的统计图(图1,图2)

根据统计图提供的信息,回答下列问题:
(1)![]() ______,
______,![]() ______.
______.
(2)在图1中,喜爱《朗读者》节目所对应的扇形的圆心角度数是______度;
(3)请根据以上信息直接在答题卡中补全图2的条形统计图;
(4)已知该校七年级共有420位学生,那么他们最喜欢《中国诗词大会》这个节目的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴交于点M.

(1)求此抛物线的解析式和对称轴;
(2)在此抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个自然数的立方,可以分裂成若干个连续奇数的和,例如:![]() ,
,![]() 和
和![]() 分别可以按如图所示的方式“分裂”成2个,3个和4个连续奇数的和,即
分别可以按如图所示的方式“分裂”成2个,3个和4个连续奇数的和,即![]() ,
,![]() ,…,若
,…,若![]() 也按照此规律来进行“分裂”,则
也按照此规律来进行“分裂”,则![]() “分裂”出的奇数中,最大的奇数是( )
“分裂”出的奇数中,最大的奇数是( )



A.39B.41C.43D.45
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.

(1)求证:AC=AE;
(2)若点E为AB的中点,CD=4,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 四边形OABC为直角梯形,A(4,0),B(3,4),C(0,4). 点![]() 从
从![]() 出发以每秒2个单位长度的速度向
出发以每秒2个单位长度的速度向![]() 运动;点
运动;点![]() 从
从![]() 同时出发,以每秒1个单位长度的速度向
同时出发,以每秒1个单位长度的速度向![]() 运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点
运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点![]() 作
作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,连结AC交NP于Q,连结MQ.
,连结AC交NP于Q,连结MQ.
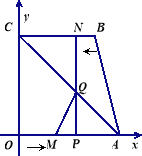
【1】点 (填M或N)能到达终点;
【1】求△AQM的面积S与运动时间t的函数关系式,并写出自变量t的取值范围,当t为何值时,S的值最大;
【1】是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标,若不存在,
![]() 说明理由.
说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在双曲线y=![]() 上,点B在双曲线y=
上,点B在双曲线y=![]() (k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )

A. 6 B. 9 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:

如图①,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.中线AD的取值范围是___________;
(2)问题解决: 如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,以C为顶点作∠ECF,使得角的两边分别交AB,AD于E、F两点,连接EF,且EF=BE+DF,试探索∠ECF与∠A之间的数量关系,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com