
ЁОЬтФПЁПЃЈ1ЃЉдФЖСРэНтЃК

ШчЭМЂйЃЌдкЁїABCжаЃЌШєAB=5ЃЌAC=3ЃЌЧѓBCБпЩЯЕФжаЯпADЕФШЁжЕЗЖЮЇ.
НтОіДЫЮЪЬтПЩвдгУШчЯТЗНЗЈЃКбгГЄADЕНЕуEЪЙDE=ADЃЌдйСЌНгBE(ЛђНЋЁїACDШЦзХЕуDФцЪБеыа§зЊ180ЁуЕУЕНЁїEBD)ЃЌАбABЃЌACЃЌ2ADМЏжадкЁїABEжаЃЌРћгУШ§НЧаЮШ§БпЕФЙиЯЕМДПЩХаЖЯ.жаЯпADЕФШЁжЕЗЖЮЇЪЧ___________ЃЛ
(2)ЮЪЬтНтОі: ШчЭМЂкЃЌдкЁїABCжа,DЪЧBCБпЩЯЕФжаЕу,DEЁЭDFгкЕуD,DEНЛABгкЕуE,DFНЛACгкЕуF,СЌНгEF,ЧѓжЄ:BE+CFЃОEFЃЛ
(3)ЮЪЬтЭиеЙ:ШчЭМЂл,дкЫФБпаЮABCDжа,ЁЯB+ЁЯD=180Ёу,CB=CD,вдCЮЊЖЅЕузїЁЯECF,ЪЙЕУНЧЕФСНБпЗжБ№НЛAB,ADгкEЁЂFСНЕу,СЌНгEF,ЧвEF=BE+DFЃЌЪдЬНЫїЁЯECFгыЁЯAжЎМфЕФЪ§СПЙиЯЕ,ВЂМгвджЄУї.
ЁОД№АИЁПЃЈ1ЃЉ1ЃМADЃМ4ЃЛЃЈ2ЃЉжЄУїМћНтЮіЃЛЃЈ3ЃЉЁЯA+2ЁЯECF=180ЁуЃЌРэгЩМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉбгГЄADЕНEЃЌЪЙDE=ADЃЌСЌНгBEЃЌжЄЁїADCЁеЁїEDBЃЌЭЦГіEB=ACЃЌИљОнШ§НЧаЮЕФШ§БпЙиЯЕЧѓГіМДПЩЃЛ
ЃЈ2ЃЉЯШРћгУASAХаЖЈЁїBGDЁеЁїCFDЃЌДгЖјЕУГіBG=CFЃЛдйРћгУШЋЕШЕФаджЪПЩЕУGD=FDЃЌдйгаDEЁЭGFЃЌДгЖјЕУГіEG=EFЃЌСНБпКЭДѓгкЕкШ§БпДгЖјЕУГіBE+CFЃОEFЃЛ
ЃЈ3ЃЉбгГЄEBЕНGЃЌЪЙBG=DFЃЌСЌНгCGЃЌЭЈЙ§SASжЄУїЁїCDFЁеЁїCBGЃЌЕУЕНCG=CFЃЌЁЯBCG=ЁЯDCFЃЌдйжЄУїЁїCEFЁеЁїCEGЃЌЕУЕНЁЯECF=ЁЯEDGЃЌгЩЁЯA+ЁЯBCD=180ЁуЃЌЭЈЙ§ЕШСПДњЛЛМДПЩЕУЕНЁЯA+2ЁЯECF=180Ёу.
ЃЈ1ЃЉбгГЄADЕНEЃЌЪЙAD=DEЃЌСЌНгBEЃЌ
ЁпADЪЧЁїABCЕФжаЯпЃЌ
ЁрBD=CDЃЌ
дкЁїADCгыЁїEDBжаЃЌ
 ЃЌ
ЃЌ
ЁрЁїADCЁеЁїEDBЃЈSASЃЉЃЌ
ЁрEB=ACЃЌ
ЁпAB=5ЃЌAC=3ЃЌ
ИљОнШ§НЧаЮЕФШ§БпЙиЯЕЕУЃКAB-ACЃМAEЃМAC+ABЃЌ
Ёр2ЃМAEЃМ8ЃЌ
ЁпAE=2AD
Ёр1ЃМADЃМ4ЃЌ
МДЃКBCБпЩЯЕФжаЯпADЕФШЁжЕЗЖЮЇ1ЃМADЃМ4ЃЌ
ЙЪД№АИЮЊЃК1ЃМADЃМ4ЃЛ
ЃЈ2ЃЉЙ§ЕуBзїBGЁЮACНЛFDЕФбгГЄЯпгкGЃЌСЌНгEGЃЌ

ЁрЁЯDBG=ЁЯDCFЃЎ
ЁпDЮЊBCЕФжаЕуЃЌ
ЁрBD=CDЃЌ
гжЁпЁЯBDG=ЁЯCDFЃЌ
ЁрЁїBGDЁеЁїCFDЃЈASAЃЉЃЎ
ЁрGD=FDЃЌBG=CFЃЌ
гжЁпDEЁЭDFЃЌ
ЁрEG=EFЃЈДЙжБЦНЗжЯпЕНЯпЖЮЖЫЕуЕФОрРыЯрЕШЃЉЃЎ
ЁрдкЁїEBGжаЃЌBE+BGЃОEGЃЌ
МДBE+CFЃОEFЃЛ
ЃЈ3ЃЉЁЯA+2ЁЯECF=180ЁуЃЌРэгЩШчЯТЃК
бгГЄEBЕНGЃЌЪЙBG=DFЃЌСЌНгCGЃЌ
ЁпЁЯD+ЁЯABC=180ЁуЃЌЁЯABC+ЁЯCBG=180ЁуЃЌ
ЁрЁЯD=ЁЯCBGЃЌ
гжЁпCD=CBЃЌDF=BGЃЌ
ЁрЁїCDFЁеЁїCBGЃЌ
ЁрCF=CGЃЌЁЯDCF=ЁЯBCGЃЌ
ЁпEF=DF+BEЃЌEG=BE+BGЃЌDF=BGЃЌ
ЁрEF=EGЃЌ
гжЁпEC=ECЃЌ
ЁрЁїCEFЁеЁїCEGЃЌ
ЁрЁЯECF=ЁЯECGЃЌ
ЁпЁЯBCD=ЁЯDCF+ЁЯBCFЃЌ
ЁрЁЯBCD=ЁЯBCF+ЁЯBCG=ЁЯFCG=ЁЯECF+ЁЯECG=2ЁЯECFЃЌ
ЁпЁЯD+ЁЯA+ЁЯABC+ЁЯBCD=360ЁуЃЌЁЯD+ЁЯABC=180ЁуЃЌ
ЁрЁЯA+ЁЯBCD=180ЁуЃЌ
ЁрЁЯA+2ЁЯECF=180Ёу.




| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпy=ЃЈxЉ1ЃЉ2+kЕФЭМЯѓгыxжсНЛгкЕуAЃЈЉ1ЃЌ0ЃЉЃЌCСНЕуЃЌгыyжсНЛгкЕуBЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпНтЮіЪНМАBЕузјБъЃЛ
ЃЈ2ЃЉдкХзЮяЯпЩЯЪЧЗёДцдкЕуPЪЙSЁїPAC=![]() SЁїABCЃПШєДцдкЃЌЧѓГіPЕузјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
SЁїABCЃПШєДцдкЃЌЧѓГіPЕузјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдкЕуQЃЌЪЙЁїABQЪЧЕШбќШ§НЧаЮЃЌШєДцдкЃЌЧѓГіQЕузјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌСНИі30ЁуЕФНЧBACгыНЧMONЃЌЖЅЕуAдкЩфЯпONЩЯФГДІЃЌЯжБЃГжНЧMONВЛЖЏЃЌНЋНЧBACШЦЕуAвдУПУы15ЁуЕФЫйЖШЫГЪБеыа§зЊЃЌБпABЁЂACЗжБ№гыБпOMНЛгкЕуPЁЂQЃЌЕБACЁЮOMЪБЃЌНЛЕуQЯћЪЇа§зЊНсЪјЁЃЩшдЫЖЏЪБМфЮЊtУыЃЈt>0ЃЉ.


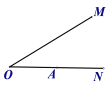

ЃЈ1ЃЉЕБt=2УыЪБЃЌOP:PQ= ЃЛ
ЃЈ2ЃЉдкдЫЖЏЕФЙ§ГЬжаЃЌЁїAPQФмЗёГЩЮЊЕШбќШ§НЧаЮЃПШєФмЃЌЧыРћгУБИгУЭМЃЌжБНгаДГіДЫЪБЕФдЫЖЏЪБМфЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉжаХаЖЯЁїOAQЕФаЮзДЃЌВЂбЁдёЦфжаЕФвЛИіЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуCдквдABЮЊжБОЖЕФАыдВЩЯЃЌAB=4ЃЌЁЯCBA=30ЁуЃЌЕуDдкAOЩЯдЫЖЏЃЌЕуEгыЕуDЙигкACЖдГЦЃКDFЁЭDEгкЕуDЃЌВЂНЛECЕФбгГЄЯпгкЕуFЃЌЯТСаНсТлЃК

ЂйCE=CFЃЛ
ЂкЯпЖЮEFЕФзюаЁжЕЮЊ![]() ЃЛ
ЃЛ
ЂлЕБAD=1ЪБЃЌEFгыАыдВЯрЧаЃЛ
ЂмЕБЕуDДгЕуAдЫЖЏЕНЕуOЪБЃЌЯпЖЮEFЩЈЙ§ЕФУцЛ§ЪЧ4![]() ЃЎ
ЃЎ
Цфжае§ШЗЕФађКХЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпЕФЖЅЕу![]() ЃЌЧвОЙ§Еу
ЃЌЧвОЙ§Еу![]() ЃЌгы
ЃЌгы![]() жсЗжБ№НЛгк
жсЗжБ№НЛгк![]() СНЕуЃЎ
СНЕуЃЎ

ЃЈ1ЃЉЧѓжБЯп![]() КЭИУХзЮяЯпЕФНтЮіЪНЃЛ
КЭИУХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌЕу![]() ЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЧвдкжБЯп
ЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЧвдкжБЯп![]() ЕФЩЯЗНЃЌЙ§Еу
ЕФЩЯЗНЃЌЙ§Еу![]() зї
зї![]() жсЕФЦНааЯпгыжБЯп
жсЕФЦНааЯпгыжБЯп![]() НЛгкЕу
НЛгкЕу![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФзюДѓжЕЃЛ
ЕФзюДѓжЕЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌ![]() жсНЛ
жсНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЪЧХзЮяЯпЩЯ
ЪЧХзЮяЯпЩЯ![]() ЁЂ
ЁЂ![]() жЎМфЕФвЛИіЖЏЕуЃЌжБЯп
жЎМфЕФвЛИіЖЏЕуЃЌжБЯп![]() ЁЂ
ЁЂ![]() гы
гы![]() ЗжБ№НЛгк
ЗжБ№НЛгк![]() ЁЂ
ЁЂ![]() ЃЌЕБЕу
ЃЌЕБЕу![]() дЫЖЏЪБЃЌЧѓ
дЫЖЏЪБЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋСНИіШЋЕШЕФЁїABCКЭЁїDBEАДЭМ1ЗНЪНАкЗХЃЌЦфжаЁЯACBЃНЁЯDEBЃН90ЁуЃЌЁЯAЃНЁЯDЃН30ЁуЃЌЕуEТфдкABЩЯЃЌDEЫљдкжБЯпНЛACЫљдкжБЯпгкFЁЃ
ЃЈ1ЃЉЧѓжЄЃКAFЃЋEFЃНDEЃЛ
ЃЈ2ЃЉШєНЋЭМ1жаЕФЁїDBEШЦЕуBЫГЪБеыа§зЊНЧІСЃЌЧв60Ёу<ІС<180ЁуЃЌЦфЫћЬѕМўВЛБфЃЌШчЭМ2ЃЌЧыжБНгаДГіДЫЪБЯпЖЮAFЃЌEFгыDEжЎМфЕФЪ§СПЙиЯЕЁЃ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћвЛИіе§ећЪ§ФмаДГЩ![]() ЕФаЮЪНЃЈЦфжаaЃЌbОљЮЊздШЛЪ§ЃЉЃЌдђГЦжЎЮЊЦХТоФІѓХЖрЪ§ЃЌБШШч7КЭ31ОљЪЧЦХТоФІѓХЖрЪ§ЃЌвђЮЊ7ЃН22ЃЋ3ЁС12ЃЌ31ЃН22ЃЋ3ЁС32ЁЃ
ЕФаЮЪНЃЈЦфжаaЃЌbОљЮЊздШЛЪ§ЃЉЃЌдђГЦжЎЮЊЦХТоФІѓХЖрЪ§ЃЌБШШч7КЭ31ОљЪЧЦХТоФІѓХЖрЪ§ЃЌвђЮЊ7ЃН22ЃЋ3ЁС12ЃЌ31ЃН22ЃЋ3ЁС32ЁЃ
ЃЈ1ЃЉЧыжЄУїЃК28КЭ217ЖМЪЧЦХТоФІѓХЖрЪ§ЁЃ
ЃЈ2ЃЉЧыжЄУїЃКШЮКЮСНИіЦХТоФІѓХЖрЪ§ЕФГЫЛ§вРОЩЪЧЦХТоФІѓХЖрЪ§ЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊA1ЃЌA2ЃЌA3ЃЌЁЃЌAnЪЧxжсЩЯЕФЕуЃЌЧвOA1ЃНA1A2ЃНA2A3ЃНA3A4ЃНЁЃНAnЃ1AnЃН1ЃЌЗжБ№Й§ЕуA1ЃЌA2ЃЌA3ЃЌЁЃЌAnзїxжсЕФДЙЯпНЛЖўДЮКЏЪ§yЃН![]() x2(xЃО0)ЕФЭМЯѓгкЕуP1ЃЌP2ЃЌP3ЃЌЁЃЌPn.ШєМЧЁїOA1P1ЕФУцЛ§ЮЊS1ЃЌЙ§ЕуP1зїP1B1ЁЭA2P2гкЕуB1ЃЌМЧЁїP1B1P2ЕФУцЛ§ЮЊS2ЃЌЙ§ЕуP2зїP2B2ЁЭA3P3гкЕуB2ЃЌМЧЁїP2B2P3ЕФУцЛ§ЮЊS3ЁЁвРДЮНјааЯТШЅЃЌзюКѓМЧЁїPnЃ1BnЃ1Pn(nЃО1)ЕФУцЛ§ЮЊSnЃЌдђSnЃН(ЁЁЁЁ)
x2(xЃО0)ЕФЭМЯѓгкЕуP1ЃЌP2ЃЌP3ЃЌЁЃЌPn.ШєМЧЁїOA1P1ЕФУцЛ§ЮЊS1ЃЌЙ§ЕуP1зїP1B1ЁЭA2P2гкЕуB1ЃЌМЧЁїP1B1P2ЕФУцЛ§ЮЊS2ЃЌЙ§ЕуP2зїP2B2ЁЭA3P3гкЕуB2ЃЌМЧЁїP2B2P3ЕФУцЛ§ЮЊS3ЁЁвРДЮНјааЯТШЅЃЌзюКѓМЧЁїPnЃ1BnЃ1Pn(nЃО1)ЕФУцЛ§ЮЊSnЃЌдђSnЃН(ЁЁЁЁ)

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАдВВФТёБкЁБЪЧЮвЙњЙХДњжјУћЕФЪ§бЇжјзїЁЖОХеТЫуЪѕЁЗжаЕФвЛИіЮЪЬтЃЌЁАНёгадВВФЃЌТёдкБкжаЃЌВЛжЊДѓаЁЃЌвдОтОтжЎЃЌЩювЛДчЃЌОтЕРГЄвЛГпЃЌЮЪОтМИКЮЃПЁБгУЯжДњЕФЪ§бЇгябдБэЪіЪЧЃКЁАШчЭМЃЌCDЮЊЁбOЕФжБОЖЃЌЯвABЁЭCDДЙзуЮЊEЃЌCE=1ДчЃЌAB=10ДчЃЌЧѓжБОЖCDЕФГЄЁБЃЌвРЬтвтЃЌCDГЄЮЊЃЈ ЃЉ

AЃЎ12Дч BЃЎ13Дч CЃЎ24Дч DЃЎ26Дч
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com