
 如图,一次函数y=-kx+n(k≠0)与x轴、y轴分别交于A、B两点,与反比例函数y=$\frac{k}{x}$(k≠0)交于C、D两点,且C、D两点分别是线段AB的三等分点,若S△AOB=$\frac{9}{4}$,则n=( )
如图,一次函数y=-kx+n(k≠0)与x轴、y轴分别交于A、B两点,与反比例函数y=$\frac{k}{x}$(k≠0)交于C、D两点,且C、D两点分别是线段AB的三等分点,若S△AOB=$\frac{9}{4}$,则n=( )| A. | -$\sqrt{2}$ | B. | -$\frac{3}{2}\sqrt{2}$ | C. | -2$\sqrt{2}$ | D. | -$\frac{5}{2}\sqrt{2}$ |
分析 令x=0,则y=-kx+n=n,令y=0,则0=-kx+n,即x=$\frac{n}{k}$,于是得到A($\frac{n}{k}$,0),B(0,n),求得OA=$\frac{n}{k}$,OB=-n,根据三角形的面积列方程$\frac{1}{2}$×$\frac{n}{k}$(-n)=$\frac{9}{4}$,得到$\frac{n}{k}=\frac{9}{2n}$,于是得到(-$\frac{9}{2n}$,0),由于C、D两点分别是线段AB的三等分点,得到C(-$\frac{3}{2n}$,$\frac{2n}{3}$)求得k=$\frac{3}{2n}$•$\frac{2n}{3}$=-1,得到△AOB是等腰直角三角形,即可得到结论.
解答 解:令x=0,则y=-kx+n=n,令y=0,则0=-kx+n,即x=$\frac{n}{k}$,
∴A($\frac{n}{k}$,0),B(0,n),
∴OA=$\frac{n}{k}$,OB=-n,
∵S△AOB=$\frac{9}{4}$,
∴$\frac{1}{2}OA•OB=\frac{9}{4}$,
即$\frac{1}{2}$×$\frac{n}{k}$(-n)=$\frac{9}{4}$,
∴k=$\frac{2}{9}{n}^{2}$,
∴$\frac{n}{k}=\frac{9}{2n}$,
∴A(-$\frac{9}{2n}$,0),
∵C、D两点分别是线段AB的三等分点,
∴C(-$\frac{3}{2n}$,$\frac{2n}{3}$)
∴k=$\frac{3}{2n}$•$\frac{2n}{3}$=-1,
∴OA=-n,
∴OA=OB,
∴△AOB是等腰直角三角形,
∴$\frac{1}{2}$(-n)2=$\frac{9}{4}$,
∴-n=$\frac{3\sqrt{2}}{2}$,
∴n=-$\frac{3\sqrt{2}}{2}$,
故选B.
点评 此题考查了反比例函数与一次函数的交点问题.此题难度较大,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:选择题
 如图,⊙O是Rt△ABC的外接圆,E是AC的中点,过E作EF⊥AB于D,交⊙O于F,交AC于M,则下列结论:①AM=ME;②DE=$\frac{1}{2}$AC;③DM=$\frac{1}{2}$EM;④OD=$\frac{1}{2}$BC,其中正确结论的序号是( )
如图,⊙O是Rt△ABC的外接圆,E是AC的中点,过E作EF⊥AB于D,交⊙O于F,交AC于M,则下列结论:①AM=ME;②DE=$\frac{1}{2}$AC;③DM=$\frac{1}{2}$EM;④OD=$\frac{1}{2}$BC,其中正确结论的序号是( )| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,线段AB的长为$30\sqrt{2}$,点D在AB上,△ACD是边长为15的等边三角形,过点D作与CD垂直的射线DP,过DP上一动点G(不与D重合)作矩形CDGH,记矩形CDGH的对角线交点为O,连接OB,则线段BO的最小值为( )
如图,线段AB的长为$30\sqrt{2}$,点D在AB上,△ACD是边长为15的等边三角形,过点D作与CD垂直的射线DP,过DP上一动点G(不与D重合)作矩形CDGH,记矩形CDGH的对角线交点为O,连接OB,则线段BO的最小值为( )| A. | $15\sqrt{2}$ | B. | 15 | C. | $30\sqrt{2}$ | D. | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,AB=AC=$\sqrt{2}$,∠BAC=90°,点D、E在线段BC上运动,设BE=x,CD=y.下列结论中一定成立的是①③④.(填写所有正确结论的序号)
如图,在Rt△ABC中,AB=AC=$\sqrt{2}$,∠BAC=90°,点D、E在线段BC上运动,设BE=x,CD=y.下列结论中一定成立的是①③④.(填写所有正确结论的序号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
| 甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | ① |
| 乙 | 10 | 7 | 10 | 10 | 9 | 8 | ② | 9.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知直线y=-2x+8与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.
如图,已知直线y=-2x+8与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
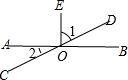 如图,直线AB和CD相交于O点,∠EOB=90°,则图中∠1与∠2的关系是( )
如图,直线AB和CD相交于O点,∠EOB=90°,则图中∠1与∠2的关系是( )| A. | ∠1与∠2互补 | B. | ∠1与∠2互余 | C. | ∠1与∠2相等 | D. | ∠1=2∠2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com