
【题目】如图,一次函数y=x+m的图象与反比例函数y=![]() 的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
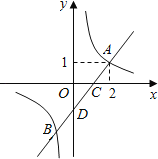
(1)求一次函数和反比例函数的解析式;
(2)求点C的坐标;
(3)结合图象直接写出不等式0<x+m≤![]() 的解集.
的解集.
【答案】(1)y=x﹣1, y=![]() ;(2)点C的坐标为(1,0);(3)1<x≤2.
;(2)点C的坐标为(1,0);(3)1<x≤2.
【解析】
(1)先把A(2,1)代入y=x+m得到m=-1;再把A(2,1)代入y=![]() 可求出k=2,从而得出一次函数和反比例函数的解析式;
可求出k=2,从而得出一次函数和反比例函数的解析式;
(2)令y=0,求得一次函数与x轴的交点坐标即为点C的坐标;
(3)观察函数图象得到不等式0<x+m≤![]() 的解集是1<x≤2.
的解集是1<x≤2.
解:(1)∵一次函数y=x+m的图象与反比例函数y=![]() 的图象交于A,B两点,点A的坐标为(2,1),
的图象交于A,B两点,点A的坐标为(2,1),
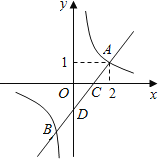
∴1=2+m,解得m=﹣1;
1=![]() ,解得k=2.
,解得k=2.
故一次函数的解析式为y=x﹣1,反比例函数的解析式为y=![]() ;
;
(2)在y=x﹣1中令y=0,则0=x﹣1,解得x=1.
故点C的坐标为(1,0);
(3)观察函数图象得到不等式0<x+m≤![]() 的解集为1<x≤2.
的解集为1<x≤2.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】课本中有一道作业题:
有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm?
小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题.
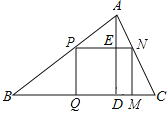
(1)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.
(2)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
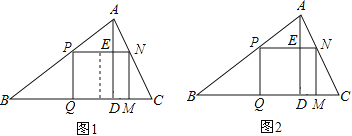
查看答案和解析>>
科目:初中数学 来源: 题型:
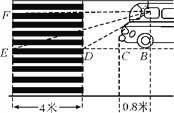
【题目】如图,某小学门口有一直线马路,交警在门口设有一条宽度为4米的斑马线,为安全起见,规定车头距斑马线后端的水平距离不得低于2米,现有一旅游车在路口遇红灯刹车停下,汽车里司机与斑马线前后两端的视角分别为∠FAE=15°和∠FAD=30°,司机距车头的水平距离为0.8米,试问该旅游车停车是否符合上述安全标准?(E,D,C,B四点在平行于斑马线的同一直线上)(参考数据:tan15°=2-![]() ,
,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象过点(1,![]() )、(2,4)、(﹣1,
)、(2,4)、(﹣1,![]() )与x轴分别交于B(左)、C两点,与y轴交于点A.
)与x轴分别交于B(左)、C两点,与y轴交于点A.
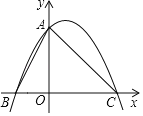
(1)求二次函数的解析式;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号.一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向.
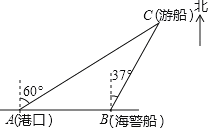
(1)求海警船距离事故船C的距离BC.
(2)若海警船以40海里/小时的速度前往救援,求海警船到达事故船C处大约所需的时间.(温馨提示:sin 53°≈0.8,cos 53°≈0.6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年重庆旅游近几年来非常火热,重庆作为国内最引人注目的“网红城市”,在国庆节期间接待游客数量高达3859万人数,远远抛离了第二名武汉,超越其1000多万游客,国庆期间某外地旅行团来重庆的网红景点打卡游览结束后旅行社对该旅行团做了一次“我最喜爱的巴渝景点”问卷调查(每名游客都填了调查表,且只选了一个景点),统计后发现洪崖洞、长江索道、李子坝轻轨站、磁器口榜上有名.其中选李子坝轻轨站的人数比进磁器口的少8人;选洪崖洞的人数不仅比磁器口的多,且为整数倍;选磁器口与洪崖洞的人数之和是选李子坝轻轨站与长江索道的人数之和的5倍;选长江索道与洪崖洞的人数之和比选李子坝轻轨站与磁器口的人数之和多24人.则该旅行团共有________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保证端午节龙舟赛在我市侨港海域顺利举办,某部门工作人员乘快艇到侨港海域考察水情,以每秒11米的速度沿平行于岸边的赛道AB由西向东行驶,在A处测得岸边一建筑物P在北偏东30°方向上,继续行驶40秒到达B处时,测得建筑物P在北偏西60°方向上,如图所示,求建筑物P到赛道AB的距离(结果保留根号).
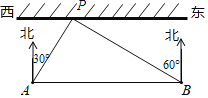
查看答案和解析>>
科目:初中数学 来源: 题型:
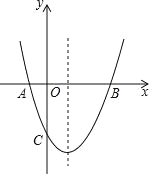
【题目】如图,抛物线y=x2﹣2x﹣3与x轴交于A,B两点(A在B的左侧),顶点为C.
(1)求A,B两点的坐标;
(2)若将该抛物线向上平移t个单位后,它与x轴恰好只有一个交点,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点。
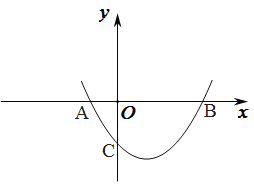
(1)求b、c的值;
(2)P为抛物线上的点,且满足S△PAB=8,求P点的坐标
(3)设抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com