
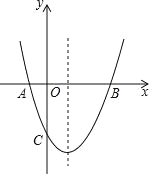
【题目】如图,抛物线y=x2﹣2x﹣3与x轴交于A,B两点(A在B的左侧),顶点为C.
(1)求A,B两点的坐标;
(2)若将该抛物线向上平移t个单位后,它与x轴恰好只有一个交点,求t的值.
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
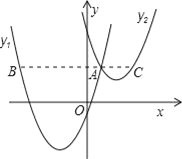
【题目】如图,抛物线y1=a(x+2)2﹣3与y2=![]() (x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
(x﹣3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:
①无论x取何值,y2的值总是正数;
②a=1;
③当x=0时,y2﹣y1=4
④2AB=3AC.
其中正确结论是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
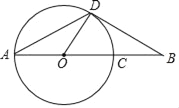
【题目】如图,线段AB经过圆心O,交⊙O于点A、C,点D为⊙O上一点,连结AD、OD、BD,∠BAD=∠B=30°.
(1)求证:BD是⊙O的切线.
(2)若OA=8,求OA、OD与![]() 围成的扇形的面积.
围成的扇形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:设一元二次方程![]() (a≠0)的两根为
(a≠0)的两根为![]() , 则两根与方程的系数之间有如下关系:
, 则两根与方程的系数之间有如下关系:![]() ,
, ![]() .根据该材料完成下列填空:
.根据该材料完成下列填空:
已知m,n是方程![]() 的两根,则
的两根,则
(1)![]() =____, mn=____;
=____, mn=____;
(2)![]() =_________.
=_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
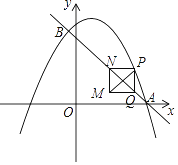
【题目】如图,在平面直角坐标系中,直线y=﹣x+3与抛物线![]() 交于A、B两点,点A在x轴上,点B的横坐标为
交于A、B两点,点A在x轴上,点B的横坐标为![]() .动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
.动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
(1)求b、c的值.
(2)当点N落在直线AB上时,直接写出m的取值范围.
(3)当点P在A、B两点之间的抛物线上运动时,设正方形PQMN的周长为C,求C与m之间的函数关系式,并写出C随m增大而增大时m的取值范围.
(4)当△PQM与坐标轴有2个公共点时,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,矩形OABC如图所示放置,点A在x轴上,点B的坐标为(n,1)(n>0),将此矩形绕O点逆时针旋转90°得到矩形OA′B′C′,抛物线y=ax2+bx+c(a≠0)经过A、A′、C′三点.
(1)求此抛物线的解析式(a、b、c可用含n的式子表示);
(2)若抛物线对称轴是x=1的一条直线,直线y=kx+2(k≠0)与抛物线相交于两点D(x1,y1)、E(x2、y2)(x1<x2),当|x1﹣x2|最小时,求抛物线与直线的交点D和E的坐标;
(3)若抛物线对称轴是x=1的一条直线,如图2,点M是抛物线的顶点,点P是y轴上一动点,点Q是坐标平面内一点,四边形APQM是以PM为对角线的平行四边形,点Q′与点Q关于直线CM对称,连接MQ′、PQ′,当△PMQ′与平行四边形APQM重合部分的面积是平行四边形的面积的![]() 时,求平行四边形APQM的面积.
时,求平行四边形APQM的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个常见铁夹的侧面示意图,OA,OB表示铁夹的两个面,C是轴,CD⊥OA于点D,已知DA=15mm,DO=24mm,DC=10mm,
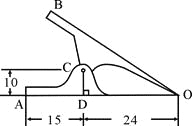
我们知道铁夹的侧面是轴对称图形,请求出A、B两点间的距离。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】手机经销商计划购进苹果手机的 iPhone8、 iphone8Plus、 iphoneX三款手机共60部,每款手机至少要购进10部,且恰好用完购机款360000元.设购进iPhone8手机![]() 部,iPhone8Plus手机
部,iPhone8Plus手机![]() 部.三款手机的进价和售价如表:
部.三款手机的进价和售价如表:
手机型号 | iPhone8 | iphone8Plus | iphoneX |
进价(元部) | 4600 | 6100 | 7600 |
售价(元部) | 5200 | 6800 | 8600 |
(1)用含![]() ,
,![]() 的式子表示购进iphoneX手机的部数.
的式子表示购进iphoneX手机的部数.
(2)求出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)假设所购进手机全部售出.
①求出预估利润![]() (元)与
(元)与![]() (部)的函数关系式.
(部)的函数关系式.
②求出预估利润的最大值,并写出此时购进三款手机各多少部.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,再填空解答:
方程![]() 的根为
的根为![]() ;
;
方程![]() 的根为
的根为![]() .
.
⑴.方程![]() 的根是
的根是![]()
![]()
⑵.若![]() 是关于x的一元二次方程
是关于x的一元二次方程![]() 的两个实数根,那么
的两个实数根,那么![]() 与系数a、b、c的关系是:
与系数a、b、c的关系是:![]()
⑶.如果![]() 是方程
是方程![]() 的两个根,根据⑵所得的结论,求
的两个根,根据⑵所得的结论,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com