【题目】如图是一个常见铁夹的侧面示意图，OA，OB表示铁夹的两个面，C是轴，CD⊥OA于点D，已知DA＝15mm，DO＝24mm，DC＝10mm，
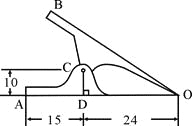
我们知道铁夹的侧面是轴对称图形，请求出A、B两点间的距离。
【答案】30mm
【解析】
解：作出示意图
连接AB，同时连结OC并延长交AB于E， …………………………………………（1＇）
因为夹子是轴对称图形，故OE是对称轴 …………………………………………（2＇）
∴OE⊥AB AE＝BE ………………………………………………（3＇）
∴Rt△OCD∽Rt△OAE ……………………………………………………（4＇）
∴
＝
…………………………………………………………………（5＇）
而OC＝
＝
＝26 ……………………………………（6＇）
即
＝
∴AE＝
＝15 ……………………（7＇）
∴AB＝2AE＝30（mm）…………………………………………………（8＇）
答：AB两点间的距离为30mm.
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】盒子里装有12张红色卡片，16张黄色卡片，4张黑色卡片和若干张蓝色卡片，每张卡片除颜色外都相同，从中任意摸出一张卡片，摸到红色卡片的概率是0.24．
（1）从中任意摸出一张卡片，摸到黑色卡片的概率是多少？
（2）求盒子里蓝色卡片的个数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】A，B两地相距80km，甲、乙两人骑车分别从A，B两地同时相向而行，他们都保持匀速行驶．如图，l1，l2分别表示甲、乙两人离B地的距离y（km）与骑车时间x（h）的函数关系．根据图象得出的下列结论，正确的个数是（ ）
①甲骑车速度为30km/小时，乙的速度为20km/小时；
②l1的函数表达式为y=80﹣30x；
③l2的函数表达式为y=20x；
④
小时后两人相遇．
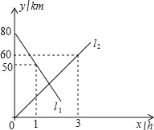
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线y＝x2﹣2x﹣3与x轴交于A，B两点（A在B的左侧），顶点为C．
（1）求A，B两点的坐标；
（2）若将该抛物线向上平移t个单位后，它与x轴恰好只有一个交点，求t的值．
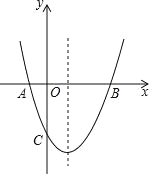
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知抛物线y＝ax2+bx+c（a≠0）的顶点坐标为Q（2，﹣1），且与y轴交于点C（0，3），与x轴交于A、B两点（点A在点B的右侧），点P是抛物线上的一动点，从点C沿抛物线向点A运动（点P与A不重合），过点P作PD∥y轴，交AC于点 D．
（1）求该抛物线的函数关系式及A、B两点的坐标；
（2）求点P在运动的过程中，线段PD的最大值；
（3）若点P与点Q重合，点E在x轴上，点F在抛物线上，问是否存在以A，P，E，F为顶点的平行四边形？若存在，直接写出点F的坐标；若不存在，请说明理由．
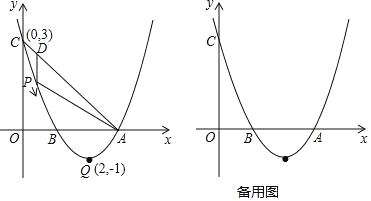
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数
的图象过点A（1，2），B（3，2），C（5，7）．若点M（-2，y1），N（-1，y2），K（8，y3）也在二次函数的图象上，则下列结论正确的是( )
A. y1＜y2＜y3 B. y2＜y1＜y3 C. y3＜y1＜y2 D. y1＜y3＜y2
查看答案和解析>>
科目：初中数学 来源： 题型：
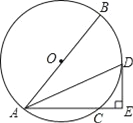
【题目】如图，已知⊙O的直径AB=10，弦AC=6，∠BAC的平分线交⊙O于点D，过点D作DE⊥AC交AC的延长线于点E．
（1）求证：DE是⊙O的切线．
（2）求DE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线
与x轴交与A(1,0),B(- 3，0)两点.
⑴求该抛物线的解析式；
⑵设⑴中的抛物线交y轴与C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由.
⑶在抛物线上BC段是否存在点P，使得△PBC面积最大，若存在，求P点坐标；若不存在，说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明参加某个智力竞答节目，答对最后两道单选题就顺利通关．第一道单选题有3个选项，第二道单选题有4个选项，这两道题小明都不会，不过小明还有一个“求助”没有用（使用“求助”可以让主持人去掉其中一题的一个错误选项）．
（1）如果小明第一题不使用“求助”，那么小明答对第一道题的概率是 ．
（2）如果小明将“求助”留在第二题使用，请用树状图或者列表来分析小明顺利通关的概率．
（3）从概率的角度分析，你建议小明在第几题使用“求助”．（直接写出答案）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com