
【题目】如图,抛物线![]() 与x轴交与A(1,0),B(- 3,0)两点.
与x轴交与A(1,0),B(- 3,0)两点.
⑴求该抛物线的解析式;
⑵设⑴中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
⑶在抛物线上BC段是否存在点P,使得△PBC面积最大,若存在,求P点坐标;若不存在,说明理由.

【答案】(1)![]() ;(2)存在,Q(-1,2);(3)存在,
;(2)存在,Q(-1,2);(3)存在,![]()
【解析】
(1)根据题意可知,将点A、B代入函数解析式,列得方程组即可求得b、c的值,求得函数解析式;
(2)根据题意可知,边AC的长是定值,要想△QAC的周长最小,即是AQ+CQ最小,所以此题的关键是确定点Q的位置,找到点A的对称点B,求得直线BC的解析式,求得与对称轴的交点即是所求;
(3)存在,设得点P的坐标,将△BCP的面积表示成二次函数,根据二次函数最值的方法即可求得点P的坐标.
(1)将A(1,0),B(-3,0)代y=-x2+bx+c中得
![]() ,
,
∴![]() .
.
∴抛物线解析式为:y=-x2-2x+3;
(2)存在.
理由如下:由题知A、B两点关于抛物线的对称轴x=-1对称,
∴直线BC与x=-1的交点即为Q点,此时△AQC周长最小,
∵y=-x2-2x+3,
∴C的坐标为:(0,3),
直线BC解析式为:y=x+3,
Q点坐标即为![]() ,
,
解得![]() ,
,
∴Q(-1,2);
(3)存在.
理由如下:设P点(x,-x2-2x+3)(-3<x<0),
∵S△BPC=S四边形BPCO-S△BOC=S四边形BPCO-![]() ,
,
若S四边形BPCO有最大值,则S△BPC就最大,
∴S四边形BPCO=S△BPE+S直角梯形PEOC,
=![]() BEPE+
BEPE+![]() OE(PE+OC)
OE(PE+OC)
=![]() (x+3)(-x2-2x+3)+
(x+3)(-x2-2x+3)+![]() (-x)(-x2-2x+3+3)
(-x)(-x2-2x+3+3)
=![]() (x+
(x+![]() )2+
)2+![]() +
+![]() ,
,
当x=-![]() 时,S四边形BPCO最大值=
时,S四边形BPCO最大值=![]() +
+![]() ,
,
∴S△BPC最大=![]() +
+![]()
![]() =
=![]() ,
,
当x=-![]() 时,-x2-2x+3=
时,-x2-2x+3=![]() ,
,
∴点P坐标为(-![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
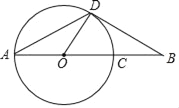
【题目】如图,线段AB经过圆心O,交⊙O于点A、C,点D为⊙O上一点,连结AD、OD、BD,∠BAD=∠B=30°.
(1)求证:BD是⊙O的切线.
(2)若OA=8,求OA、OD与![]() 围成的扇形的面积.
围成的扇形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个常见铁夹的侧面示意图,OA,OB表示铁夹的两个面,C是轴,CD⊥OA于点D,已知DA=15mm,DO=24mm,DC=10mm,
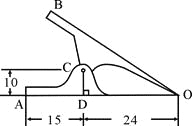
我们知道铁夹的侧面是轴对称图形,请求出A、B两点间的距离。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】手机经销商计划购进苹果手机的 iPhone8、 iphone8Plus、 iphoneX三款手机共60部,每款手机至少要购进10部,且恰好用完购机款360000元.设购进iPhone8手机![]() 部,iPhone8Plus手机
部,iPhone8Plus手机![]() 部.三款手机的进价和售价如表:
部.三款手机的进价和售价如表:
手机型号 | iPhone8 | iphone8Plus | iphoneX |
进价(元部) | 4600 | 6100 | 7600 |
售价(元部) | 5200 | 6800 | 8600 |
(1)用含![]() ,
,![]() 的式子表示购进iphoneX手机的部数.
的式子表示购进iphoneX手机的部数.
(2)求出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)假设所购进手机全部售出.
①求出预估利润![]() (元)与
(元)与![]() (部)的函数关系式.
(部)的函数关系式.
②求出预估利润的最大值,并写出此时购进三款手机各多少部.
查看答案和解析>>
科目:初中数学 来源: 题型:
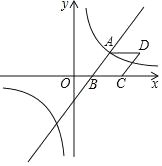
【题目】如图,已知一次函数y=![]() x﹣3与反比例函数y=
x﹣3与反比例函数y=![]() 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.
(1)填空:n的值为____,k的值为______;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比例函数y=![]() 的图象,当y≥﹣3时,请直接写出自变量x的取值范围.
的图象,当y≥﹣3时,请直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
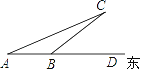
【题目】如图,一艘轮船以18海里/时的速度由西向东航行,在A处测得小岛C在北偏东75°方向上,两小时后,轮船在B处测得小岛C在北偏东60°方向上,在小岛周围15海里处有暗礁,若轮船仍然按18海里/时的速度向东航行,请问是否有触礁危险?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量出楼房AC的高度,从距离楼底C处![]() 米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:
米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:![]() 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈![]() ,计算结果用根号表示,不取近似值).
,计算结果用根号表示,不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,再填空解答:
方程![]() 的根为
的根为![]() ;
;
方程![]() 的根为
的根为![]() .
.
⑴.方程![]() 的根是
的根是![]()
![]()
⑵.若![]() 是关于x的一元二次方程
是关于x的一元二次方程![]() 的两个实数根,那么
的两个实数根,那么![]() 与系数a、b、c的关系是:
与系数a、b、c的关系是:![]()
⑶.如果![]() 是方程
是方程![]() 的两个根,根据⑵所得的结论,求
的两个根,根据⑵所得的结论,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
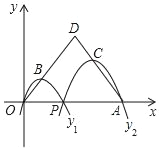
【题目】如图,已知△AOD是等腰三角形,点A(12,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P,O两点的二次函数y1,和过P、A两点的二次函数y2,的开口均向下,它们的顶点分别为B,C,点B,C分别在OD、AD上.当OD=AD=10时,则两个二次函数的最大值之和等于_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com