
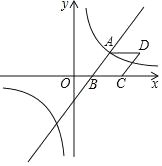
【题目】如图,已知一次函数y=![]() x﹣3与反比例函数y=
x﹣3与反比例函数y=![]() 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.
(1)填空:n的值为____,k的值为______;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比例函数y=![]() 的图象,当y≥﹣3时,请直接写出自变量x的取值范围.
的图象,当y≥﹣3时,请直接写出自变量x的取值范围.
【答案】(1)3;12;(2)点D的坐标为(4+![]() ,3);(3)x≤﹣4或x>0.
,3);(3)x≤﹣4或x>0.
【解析】
(1)把点A(4,n)代入一次函数y=![]() x-3,得到n的值为3;再把点A(4,3)代入反比例函数y=
x-3,得到n的值为3;再把点A(4,3)代入反比例函数y=![]() ,得到k的值为12;
,得到k的值为12;
(2)根据坐标轴上点的坐标特征可得点B的坐标为(2,0),过点A作AE⊥x轴,垂足为E,过点D作DF⊥x轴,垂足为F,根据勾股定理得到AB=![]() ,根据AAS可得△ABE≌△DCF,根据菱形的性质和全等三角形的性质可得点D的坐标;
,根据AAS可得△ABE≌△DCF,根据菱形的性质和全等三角形的性质可得点D的坐标;
(3)根据反比例函数的性质即可得到当y≥-3时,自变量x的取值范围.
解:(1)把点A(4,n)代入一次函数y=![]() x﹣3,
x﹣3,
可得n=![]() ×4﹣3=3;
×4﹣3=3;
把点A(4,3)代入反比例函数y=![]() ,
,
可得3=![]() ,
,
解得k=12.
故答案为:3,12.
(2)∵一次函数y=![]() x﹣3与x轴相交于点B,
x﹣3与x轴相交于点B,
∴![]() x﹣3=0,
x﹣3=0,
解得x=2,
∴点B的坐标为(2,0),
如图,过点A作AE⊥x轴,垂足为E,
过点D作DF⊥x轴,垂足为F,
∵A(4,3),B(2,0),
∴OE=4,AE=3,OB=2,
∴BE=OE﹣OB=4﹣2=2,
在Rt△ABE中,
AB=![]() ,
,
∵四边形ABCD是菱形,
∴AB=CD=BC=![]() ,AB∥CD,
,AB∥CD,
∴∠ABE=∠DCF,
∵AE⊥x轴,DF⊥x轴,
∴∠AEB=∠DFC=90°,
在△ABE与△DCF中,
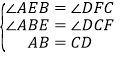 ,
,
∴△ABE≌△DCF(ASA),
∴CF=BE=2,DF=AE=3,
∴OF=OB+BC+CF=2+![]() +2=4+
+2=4+![]() ,
,
∴点D的坐标为(4+![]() ,3).
,3).
(3)当y=﹣3时,﹣3=![]() ,
,
解得x=﹣4.
故当y≥﹣3时,自变量x的取值范围是x≤﹣4或x>0.


科目:初中数学 来源: 题型:
【题目】动物学家通过大量的调查估计出,某种动物活到20岁的概率为0.8,活到25岁的概率是0.5,活到30岁的概率是0.3.现年20岁的这种动物活到25岁的概率为多少?现年25岁的这种动物活到30岁的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
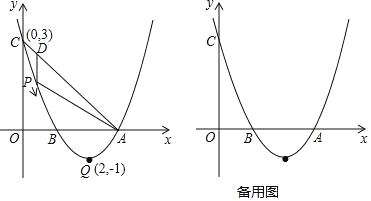
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,﹣1),且与y轴交于点C(0,3),与x轴交于A、B两点(点A在点B的右侧),点P是抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点 D.
(1)求该抛物线的函数关系式及A、B两点的坐标;
(2)求点P在运动的过程中,线段PD的最大值;
(3)若点P与点Q重合,点E在x轴上,点F在抛物线上,问是否存在以A,P,E,F为顶点的平行四边形?若存在,直接写出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
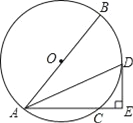
【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线.
(2)求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
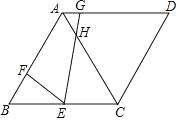
【题目】如图,在菱形ABCD中,∠B=60°,BC=6,E为BC中点,F是AB上一点,G为AD上一点,且BF=2,∠FEG=60°,EG交AC于点H,下列结论:①△BEF∽△CHE;②AG=1;③EH=![]() ;④S△BEF=3S△AGH;正确的是______.(填序号即可)
;④S△BEF=3S△AGH;正确的是______.(填序号即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交与A(1,0),B(- 3,0)两点.
与x轴交与A(1,0),B(- 3,0)两点.
⑴求该抛物线的解析式;
⑵设⑴中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
⑶在抛物线上BC段是否存在点P,使得△PBC面积最大,若存在,求P点坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,取一根9.5 m长的标杆AB,在其上系一活动旗帜C,使标杆的影子落在平地和一堤坝的左斜坡上,拉动旗帜使其影子正好落在斜坡底角顶点D处.若测得旗高BC=4.5 m,影长BD=9 m,影长DE=5 m,请计算左斜坡的坡比(假设标杆的影子BD,DE均与坝底线DM垂直).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制成下面两幅不完整的统计图,请你根据图中提供的信息解答下列问题:

(1)在这次调查中,一共调查了 名学生;
(2)补全条形统计图;
(3)若该校共有1500名学生,估计爱好运动的学生有 人;
(4)在全校同学中随机选取一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com