[题目]下列方程中.无论a取何值时.总是关于x的一元二次方程的是( )A. B. C. D. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】下列方程中，无论a取何值时，总是关于x的一元二次方程的是（）

A. B.

C. D.

【答案】D

【解析】

本题根据一元二次方程的定义解答．一元二次方程必须满足四个条件：（1）未知数的最高次数是2；（2）二次项系数不为0；（3）是整式方程；（4）含有一个未知数．由这四个条件对四个选项进行验证，满足这四个条件者为正确答案．

A、原方程可化为：（2a-3）x2+6a-1=0，当2a-3=0，即a=时，原方程不是一元二次方程，错误；

B、当二次项系数a=0时，方程不是一元二次方程，错误；

C、原方程可化为：（a-1）x2+x+1=0，当a-1=0，即a=1时，原方程不是一元二次方程，错误；

D、由于a2+1＞0，故原方程是一元二次方程，正确．

故选：D．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

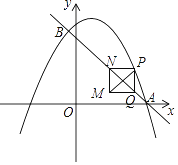
【题目】如图，在平面直角坐标系中，直线y=﹣x+3与抛物线交于A、B两点，点A在x轴上，点B的横坐标为．动点P在抛物线上运动（不与点A、B重合），过点P作y轴的平行线，交直线AB于点Q．当PQ不与y轴重合时，以PQ为边作正方形PQMN，使MN与y轴在PQ的同侧，连结PM．设点P的横坐标为m．

（1）求b、c的值．

（2）当点N落在直线AB上时，直接写出m的取值范围．

（3）当点P在A、B两点之间的抛物线上运动时，设正方形PQMN的周长为C，求C与m之间的函数关系式，并写出C随m增大而增大时m的取值范围．

（4）当△PQM与坐标轴有2个公共点时，直接写出m的取值范围．

查看答案和解析>>

科目：初中数学 来源： 题型：

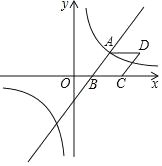
【题目】如图，已知一次函数y＝x﹣3与反比例函数y＝的图象相交于点A（4，n），与x轴相交于点B．

（1）填空：n的值为____，k的值为______；

（2）以AB为边作菱形ABCD，使点C在x轴正半轴上，点D在第一象限，求点D的坐标；

（3）观察反比例函数y＝的图象，当y≥﹣3时，请直接写出自变量x的取值范围．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，为了测量出楼房AC的高度，从距离楼底C处米的点D（点D与楼底C在同一水平面上）出发，沿斜面坡度为i=1：的斜坡DB前进30米到达点B，在点B处测得楼顶A的仰角为53°，求楼房AC的高度（参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈，计算结果用根号表示，不取近似值）．