
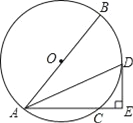
【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线.
(2)求DE的长.
【答案】(1)详见解析;(2)4.
【解析】
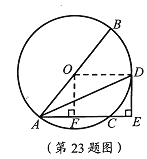
试题(1)连结OD,由AD平分∠BAC,OA=OD,可证得∠ODA=∠DAE,由平行线的性质可得OD∥AE,再由DE⊥AC即可得OE⊥DE,即DE是⊙O的切线;(2)过点O作OF⊥AC于点F,由垂径定理可得AF=CF=3,再由勾股定理求得OF=4,再判定四边形OFED是矩形,即可得DE=OF=4.
试题解析:
(1)连结OD,
∵AD平分∠BAC,
∴∠DAE=∠DAB,
∵OA=OD,
∴∠ODA=∠DAO,
∴∠ODA=∠DAE,
∴OD∥AE,
∵DE⊥AC
∴OE⊥DE
∴DE是⊙O的切线;
(2)过点O作OF⊥AC于点F,
∴AF=CF=3,
∴OF=![]() ,
,
∵∠OFE=∠DEF=∠ODE=90°,
∴四边形OFED是矩形,
∴DE=OF=4.


科目:初中数学 来源: 题型:
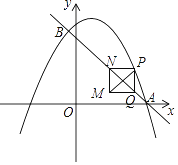
【题目】如图,在平面直角坐标系中,直线y=﹣x+3与抛物线![]() 交于A、B两点,点A在x轴上,点B的横坐标为
交于A、B两点,点A在x轴上,点B的横坐标为![]() .动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
.动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
(1)求b、c的值.
(2)当点N落在直线AB上时,直接写出m的取值范围.
(3)当点P在A、B两点之间的抛物线上运动时,设正方形PQMN的周长为C,求C与m之间的函数关系式,并写出C随m增大而增大时m的取值范围.
(4)当△PQM与坐标轴有2个公共点时,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个常见铁夹的侧面示意图,OA,OB表示铁夹的两个面,C是轴,CD⊥OA于点D,已知DA=15mm,DO=24mm,DC=10mm,
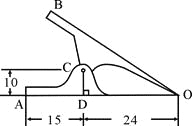
我们知道铁夹的侧面是轴对称图形,请求出A、B两点间的距离。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:甲、乙两车分别从相距200千米的![]() ,
,![]() 两地同时出发相向而行,其中甲车到
两地同时出发相向而行,其中甲车到![]() 地后立即返回,下图是它们离各自出发地的距离
地后立即返回,下图是它们离各自出发地的距离![]() (千米)与行驶时间
(千米)与行驶时间![]() (小时)之间的函数图象.
(小时)之间的函数图象.
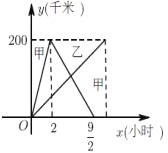
(1)求甲车离出发地的距离![]() (千米)与行驶时间
(千米)与行驶时间![]() (小时)之间的函数关系式,并写出自变量的取值范围.
(小时)之间的函数关系式,并写出自变量的取值范围.
(2)当![]() 时,甲、乙两车离各自出发地的距离相等,求乙车离出发地的距离
时,甲、乙两车离各自出发地的距离相等,求乙车离出发地的距离![]() (千米)与行驶时间
(千米)与行驶时间![]() (小时)之间的函数关系式,并写出自变量的取值范围.
(小时)之间的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,求它们在行驶的过程中相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】手机经销商计划购进苹果手机的 iPhone8、 iphone8Plus、 iphoneX三款手机共60部,每款手机至少要购进10部,且恰好用完购机款360000元.设购进iPhone8手机![]() 部,iPhone8Plus手机
部,iPhone8Plus手机![]() 部.三款手机的进价和售价如表:
部.三款手机的进价和售价如表:
手机型号 | iPhone8 | iphone8Plus | iphoneX |
进价(元部) | 4600 | 6100 | 7600 |
售价(元部) | 5200 | 6800 | 8600 |
(1)用含![]() ,
,![]() 的式子表示购进iphoneX手机的部数.
的式子表示购进iphoneX手机的部数.
(2)求出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)假设所购进手机全部售出.
①求出预估利润![]() (元)与
(元)与![]() (部)的函数关系式.
(部)的函数关系式.
②求出预估利润的最大值,并写出此时购进三款手机各多少部.
查看答案和解析>>
科目:初中数学 来源: 题型:
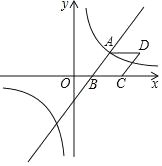
【题目】如图,已知一次函数y=![]() x﹣3与反比例函数y=
x﹣3与反比例函数y=![]() 的图象相交于点A(4,n),与x轴相交于点B.
的图象相交于点A(4,n),与x轴相交于点B.
(1)填空:n的值为____,k的值为______;
(2)以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,求点D的坐标;
(3)观察反比例函数y=![]() 的图象,当y≥﹣3时,请直接写出自变量x的取值范围.
的图象,当y≥﹣3时,请直接写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量出楼房AC的高度,从距离楼底C处![]() 米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:
米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:![]() 的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈
的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈![]() ,计算结果用根号表示,不取近似值).
,计算结果用根号表示,不取近似值).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com