
����Ŀ����֪���ס��������ֱ�����200ǧ��![]() ��
��![]() ����ͬʱ����������У����м׳���
����ͬʱ����������У����м׳���![]() �غ��������أ���ͼ����������Գ����صľ���
�غ��������أ���ͼ����������Գ����صľ���![]() ��ǧ�ף�����ʻʱ��
��ǧ�ף�����ʻʱ��![]() ��Сʱ��֮��ĺ���ͼ��
��Сʱ��֮��ĺ���ͼ��
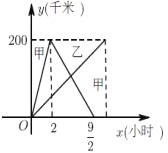
��1����׳�������صľ���![]() ��ǧ�ף�����ʻʱ��
��ǧ�ף�����ʻʱ��![]() ��Сʱ��֮��ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��Сʱ��֮��ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��2����![]() ʱ���ס�����������Գ����صľ�����ȣ����ҳ�������صľ���
ʱ���ס�����������Գ����صľ�����ȣ����ҳ�������صľ���![]() ��ǧ�ף�����ʻʱ��
��ǧ�ף�����ʻʱ��![]() ��Сʱ��֮��ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��Сʱ��֮��ĺ�����ϵʽ����д���Ա�����ȡֵ��Χ��
��3���ڣ�2���������£�����������ʻ�Ĺ�����������ʱ�䣮
���𰸡���1��![]()
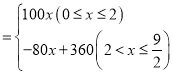 ����2��
����2��![]() ����3������
����3������![]() ��4Сʱ���ס�����������
��4Сʱ���ס�����������
��������
��1������ͼ���֪����0��x��2��2��x��![]() ���Σ����ô���ϵ�������һ�κ�������ʽ��
���Σ����ô���ϵ�������һ�κ�������ʽ��
��2�����ݣ�1�����������ʽ�����ֱ�ߵĽ������꣬�����ô���ϵ��������ҳ�������صľ���y��ǧ�ף�����ʻʱ��x��Сʱ��֮��ĺ�����ϵʽ��
��3����0��x��2��2��x��![]() ����������ֱ��г�������⼴�ɣ�
����������ֱ��г�������⼴�ɣ�
�⣺��1����0��x��2ʱ����y=mx��
��2m=200�����m=100��
���ԣ�y=100x��
��2��x��![]() ʱ����y=kx+b��
ʱ����y=kx+b��
��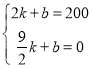 �����
�����![]() ��
��
��y=-80x+360��
��׳�������صľ���y��ǧ�ף�����ʻʱ��x��Сʱ��֮��ĺ�����ϵʽΪ�� 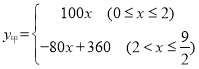 ��
��
��2����x=3ʱ��y��=-80��3+360=120��
��������ͼ�������Ϊ��3��120����
��y��=px��
����3��120�����룬��3p=120��
��ã�p=40��
���ҳ�������صľ���y��ǧ�ף�����ʻʱ��x��Сʱ��֮��ĺ�����ϵʽΪ��y��=40x��0��x��5����
��3���ٵ�![]() ʱ��������ã�
ʱ��������ã�![]() ��
��
��ã�![]() ��
��
�ڵ�![]() ʱ��������ã�
ʱ��������ã�![]() ��
��
��ã�![]() ��
��
�ྭ��![]() ��4Сʱ���ס�������������
��4Сʱ���ס�������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CD�ǰ뾶Ϊ5�ġ�O����������AB=8��CD=6��MN��ֱ����AB��MN�ڵ�E��CD��MN�ڵ�F��PΪEF�ϵ�����һ������PA+PC����СֵΪ______��
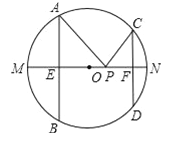
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̽�Ӧ���⣺
ij��߳�����һ����ߣ����տ��ƹ̶��ɱ����۴�����ԭ��ʹ����������ܹ���ʱ�۳������г����飺ÿ����߰�![]() Ԫ����ʱ��ÿ�������
Ԫ����ʱ��ÿ�������![]() ���������۵���ÿ����Ԫ��ÿ��ɶ��۳�
���������۵���ÿ����Ԫ��ÿ��ɶ��۳�![]() ��.��֪ÿ����ߵĹ̶��ɱ�Ϊ
��.��֪ÿ����ߵĹ̶��ɱ�Ϊ![]() Ԫ����������ߵ����۵���Ϊ����Ԫʱ������ÿ��ɻ�����
Ԫ����������ߵ����۵���Ϊ����Ԫʱ������ÿ��ɻ�����![]() Ԫ��
Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y��ax2+bx+c��a��0���Ķ�������ΪQ��2����1��������y�ύ�ڵ�C��0��3������x�ύ��A��B���㣨��A�ڵ�B���Ҳࣩ����P���������ϵ�һ���㣬�ӵ�C�����������A�˶�����P��A���غϣ�������P��PD��y�ᣬ��AC�ڵ� D��
��1����������ߵĺ�����ϵʽ��A��B��������ꣻ
��2�����P���˶��Ĺ����У��߶�PD�����ֵ��
��3������P���Q�غϣ���E��x���ϣ���F���������ϣ����Ƿ������A��P��E��FΪ�����ƽ���ı��Σ������ڣ�ֱ��д����F�����ꣻ�������ڣ���˵�����ɣ�
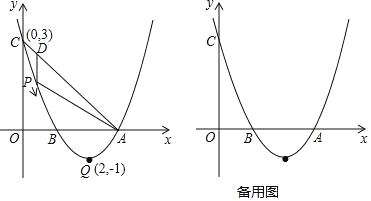
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������12�֣�
��֪����Rt��ABC��Rt��DEF����ͼ��1���ڷţ���C���E�غϣ�����B��C��E����F��ͬһ��ֱ���ϣ���ACB = ��EDF = 90�㣬��DEF = 45����AC = 8 cm��BC = 6 cm��EF = 9 cm��
��ͼ��2������DEF��ͼ��1����λ�ó�������1 cm/s���ٶ���CB����ABC��������������DEF������ͬʱ����P����ABC�Ķ���B��������2 cm/s���ٶ���BA���A��������.����DEF�Ķ���D�ƶ���AC����ʱ����DEFֹͣ��������PҲ��ֹ֮ͣ�ƶ���DE��AC�ཻ�ڵ�Q������PQ��������ʱ��Ϊt��s����0��t��4.5����
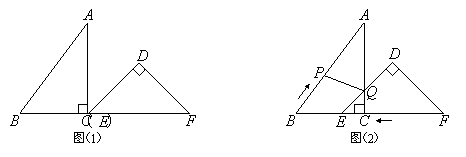
����������⣺
��1����tΪ��ֵʱ����A���߶�PQ�Ĵ�ֱƽ�����ϣ�
��2������PE�����ı���APEC�����Ϊy��cm2������y��t֮��ĺ�����ϵʽ���Ƿ����ijһʱ��t��ʹ���y��С�������ڣ����y����Сֵ���������ڣ�˵�����ɣ�
��3���Ƿ����ijһʱ��t��ʹP��Q��F������ͬһ��ֱ���ϣ������ڣ������ʱt��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��O��ֱ��AB=10����AC=6����BAC��ƽ���߽���O�ڵ�D������D��DE��AC��AC���ӳ����ڵ�E��
��1����֤��DE�ǡ�O�����ߣ�
��2����DE�ij���
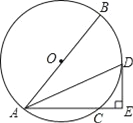
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���B��60�㣬BC��6��EΪBC�е㣬F��AB��һ�㣬GΪAD��һ�㣬��BF��2����FEG��60�㣬EG��AC�ڵ�H�����н������١�BEF�ס�CHE����AG��1����EH��![]() ����S��BEF��3S��AGH����ȷ����______��������ż��ɣ�
����S��BEF��3S��AGH����ȷ����______��������ż��ɣ�
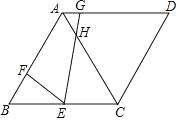
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ȡһ��9.5 m���ı��AB��������ϵһ�����C��ʹ��˵�Ӱ������ƽ�غ�һ�̰ӵ���б��������������ʹ��Ӱ����������б�µǶ���D������������BC��4.5 m��Ӱ��BD��9 m��Ӱ��DE��5 m���������б�µ��±�(�����˵�Ӱ��BD��DE����ӵ���DM��ֱ)��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ij�ο����У����мס��ҡ���3��ͬѧ�����ĿƲ���ʵ�ʳɼ����±�������λ���֣�
���� | ��ѧ | Ӣ�� | ��ѧ | |
�� | 95 | 95 | 80 | 150 |
�� | 105 | 90 | 90 | 139 |
�� | 100 | 100 | 85 | 139 |
�������б���2�ˣ������ƽ�����ĽǶȷ����������˽������
��2��Ϊ�����ֿ�ѧ���죬������Ե����ġ���ѧ��Ӣ���ѧʵ�ʳɼ�����2:3:2:3�ı��������ۺ�ƽ������������ۺ�ƽ�����ĽǶȷ����������˽������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com