
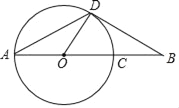
【题目】如图,线段AB经过圆心O,交⊙O于点A、C,点D为⊙O上一点,连结AD、OD、BD,∠BAD=∠B=30°.
(1)求证:BD是⊙O的切线.
(2)若OA=8,求OA、OD与![]() 围成的扇形的面积.
围成的扇形的面积.
 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:
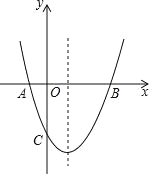
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中不正确的是( )
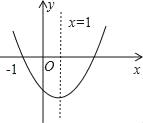
A. c<0
B. y的最小值为负值
C. 当x>1时,y随x的增大而减小
D. x=3是关于x的方程ax2+bx+c=0的一个根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盒子里装有12张红色卡片,16张黄色卡片,4张黑色卡片和若干张蓝色卡片,每张卡片除颜色外都相同,从中任意摸出一张卡片,摸到红色卡片的概率是0.24.
(1)从中任意摸出一张卡片,摸到黑色卡片的概率是多少?
(2)求盒子里蓝色卡片的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时时间t秒.

(1)求点C的坐标;
(2)当∠BCP=15°时,求t的值;
(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动物学家通过大量的调查估计出,某种动物活到20岁的概率为0.8,活到25岁的概率是0.5,活到30岁的概率是0.3.现年20岁的这种动物活到25岁的概率为多少?现年25岁的这种动物活到30岁的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
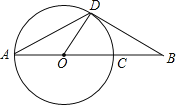
【题目】如图,线段AB经过圆心O,交⊙O于点A、C,点D为⊙O上一点,连结AD、OD、BD,∠BAD=∠B=30°.
(1)求证:BD是⊙O的切线.
(2)若OA=8,求OA、OD与弧AD围成的扇形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
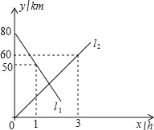
【题目】A,B两地相距80km,甲、乙两人骑车分别从A,B两地同时相向而行,他们都保持匀速行驶.如图,l1,l2分别表示甲、乙两人离B地的距离y(km)与骑车时间x(h)的函数关系.根据图象得出的下列结论,正确的个数是( )
①甲骑车速度为30km/小时,乙的速度为20km/小时;
②l1的函数表达式为y=80﹣30x;
③l2的函数表达式为y=20x;
④![]() 小时后两人相遇.
小时后两人相遇.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣2x﹣3与x轴交于A,B两点(A在B的左侧),顶点为C.
(1)求A,B两点的坐标;
(2)若将该抛物线向上平移t个单位后,它与x轴恰好只有一个交点,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交与A(1,0),B(- 3,0)两点.
与x轴交与A(1,0),B(- 3,0)两点.
⑴求该抛物线的解析式;
⑵设⑴中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
⑶在抛物线上BC段是否存在点P,使得△PBC面积最大,若存在,求P点坐标;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com