
【题目】阅读材料:设一元二次方程![]() (a≠0)的两根为
(a≠0)的两根为![]() , 则两根与方程的系数之间有如下关系:
, 则两根与方程的系数之间有如下关系:![]() ,
, ![]() .根据该材料完成下列填空:
.根据该材料完成下列填空:
已知m,n是方程![]() 的两根,则
的两根,则
(1)![]() =____, mn=____;
=____, mn=____;
(2)![]() =_________.
=_________.
【答案】(1)2012 ,2013;(2)2.
【解析】
(1)根据根与系数的关系即可得出m+n=2012、mn=2013,此题得解;
(2)由m,n是方程x2-2012x+2013=0的两根,即可得出m2-2012m+2013=0、n2-2012n+2013=0,(m2-2013m+2014)(n2-2013n+2014)即可变形为1+mn-(m+n),代入数据即可得出结论.
(1)∵m,n是方程x2-2012x+2013=0的两根,
∴m+n=2012,mn=2013,
(2) ∵m,n是方程x2-2012x+2013=0的两根,
∴m2-2012m+2013=0, n2-2012n+2013=0,
∴m2-2013m+2014=m2-2012m+2013+1-m=0+1-m=1-m;
n2-2013n+2014=n2-2012n+2013+1-n=0+1-n=1-n;
∴(m2-2013m+2014)(n2-2013n+2014)
=(1-m)(1-n)
=1-(m+n)+mn
=1-2012+2013
=2.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
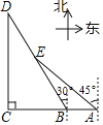
【题目】如图为某景区五个景点A,B,C,D,E的平面示意图,B,A在C的正东方向,D在C的正北方向,D,E在B的北偏西30°方向上,E在A的西北方向上,C,D相距1000![]() m,E在BD的中点处.
m,E在BD的中点处.
(1)求景点B,E之间的距离;
(2)求景点B,A之间的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时时间t秒.

(1)求点C的坐标;
(2)当∠BCP=15°时,求t的值;
(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
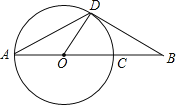
【题目】如图,线段AB经过圆心O,交⊙O于点A、C,点D为⊙O上一点,连结AD、OD、BD,∠BAD=∠B=30°.
(1)求证:BD是⊙O的切线.
(2)若OA=8,求OA、OD与弧AD围成的扇形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两地相距80km,甲、乙两人骑车分别从A,B两地同时相向而行,他们都保持匀速行驶.如图,l1,l2分别表示甲、乙两人离B地的距离y(km)与骑车时间x(h)的函数关系.根据图象得出的下列结论,正确的个数是( )
①甲骑车速度为30km/小时,乙的速度为20km/小时;
②l1的函数表达式为y=80﹣30x;
③l2的函数表达式为y=20x;
④![]() 小时后两人相遇.
小时后两人相遇.
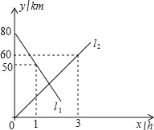
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系y=mx2+20x+n,其图象如图所示.
(1)m=_____,n=_____.
(2)销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?
(3)该种商品每天的销售利润不低于16元时,直接写出x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
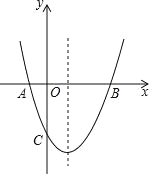
【题目】如图,抛物线y=x2﹣2x﹣3与x轴交于A,B两点(A在B的左侧),顶点为C.
(1)求A,B两点的坐标;
(2)若将该抛物线向上平移t个单位后,它与x轴恰好只有一个交点,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象过点A(1,2),B(3,2),C(5,7).若点M(-2,y1),N(-1,y2),K(8,y3)也在二次函数
的图象过点A(1,2),B(3,2),C(5,7).若点M(-2,y1),N(-1,y2),K(8,y3)也在二次函数![]() 的图象上,则下列结论正确的是( )
的图象上,则下列结论正确的是( )
A. y1<y2<y3 B. y2<y1<y3 C. y3<y1<y2 D. y1<y3<y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚准备用一段长50米的篱笆围成一个三角形形状的场地,用于饲养鸡,已知第一条边长为m米,由于条件限制第二条边长只能比第一条边长的3倍少2米.
(1)用含m的式子表示第三条边长;
(2)第一条边长能否为10米?为什么?
(3)若第一条边长最短,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com