
分析 先根据高斯求和公式把算式变形为$\frac{2}{1×2}$+$\frac{2}{2×3}$+$\frac{2}{3×4}$+…+$\frac{2}{50×51}$,然后再根据分数的拆项公式$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$拆项后通过加减相互抵消即可简算.
解答 解:1+$\frac{1}{1+2}$+$\frac{1}{1+2+3}$+$\frac{1}{1+2+3+4}$+…+$\frac{1}{1+2+3+…+50}$
=$\frac{2}{1×2}$+$\frac{2}{2×3}$+$\frac{2}{3×4}$+…+$\frac{2}{50×51}$
=2×(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{50}$-$\frac{1}{51}$)
=2×(1-$\frac{1}{51}$)
=2×$\frac{50}{51}$
=$\frac{100}{51}$.
故答案为:$\frac{100}{51}$.
点评 本题考查了有理数的混合运算,关键是熟练掌握高斯求和公式和分数拆项公式$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$的综合应用.


科目:初中数学 来源: 题型:选择题
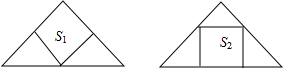 如图,将两张全等的等腰直角三角形纸片按如下两种方法剪成正方形,其面积分别为是S1、S2,则( )
如图,将两张全等的等腰直角三角形纸片按如下两种方法剪成正方形,其面积分别为是S1、S2,则( )| A. | S1>S2 | B. | S1<S2 | C. | S1=S2 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
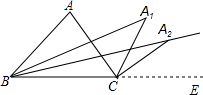 如图所示,△ABC内角∠ABC的平分线与外角∠ACE的角平分线交于点A1.
如图所示,△ABC内角∠ABC的平分线与外角∠ACE的角平分线交于点A1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com