
分析 设方程5x2+2x-3两个为x1,x2,根据根与系数的关系得到x1+x2=-$\frac{2}{5}$,x1•x2=-$\frac{3}{5}$,再分别计算-$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$和-$\frac{1}{{x}_{1}}$•(-$\frac{1}{{x}_{2}}$),然后根据根与系数的关系写出以-$\frac{1}{{x}_{1}}$和-$\frac{1}{{x}_{2}}$为两根的一元二次方程.
解答 解:设方程5x2+2x-3两个为x1,x2,
则x1+x2=-$\frac{2}{5}$,x1•x2=-$\frac{3}{5}$,
-$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$=-$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{2}{3}$和-$\frac{1}{{x}_{1}}$•(-$\frac{1}{{x}_{2}}$)=$\frac{1}{{x}_{1}{x}_{2}}$=-$\frac{5}{3}$,
所以以-$\frac{1}{{x}_{1}}$和-$\frac{1}{{x}_{2}}$为两根的一元二次方程为x2+$\frac{2}{3}$x-$\frac{5}{3}$=0.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
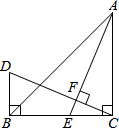 在△ABC中,∠ACB=90°,E是BC边上的一点,过C作CF⊥AE,垂足为F,过点B作BD⊥BC,交CF的延长线于点D,若∠D=65°,求∠EAC的度数.
在△ABC中,∠ACB=90°,E是BC边上的一点,过C作CF⊥AE,垂足为F,过点B作BD⊥BC,交CF的延长线于点D,若∠D=65°,求∠EAC的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
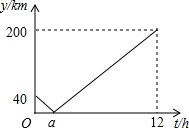 甲、乙两车要从M地沿同一条公路运输一批物资到N地,乙车比甲车先行驶1h,设甲车与乙车之间的距离为y(单位:km),甲车行驶时间为t(单位:h),y与t之间的函数关系如图所示(假设甲、乙两车速度始终保持不变).结合图象解答下列问题:
甲、乙两车要从M地沿同一条公路运输一批物资到N地,乙车比甲车先行驶1h,设甲车与乙车之间的距离为y(单位:km),甲车行驶时间为t(单位:h),y与t之间的函数关系如图所示(假设甲、乙两车速度始终保持不变).结合图象解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com