
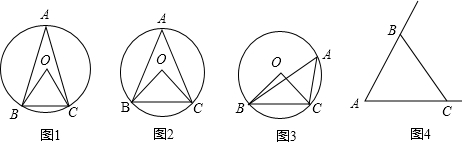
分析 (1)作OD⊥BC于D,根据垂径定理和等腰三角形的性质求得∠BOD=∠A,解直角三角形即可求得;
(2)作OD⊥BC于D,根据垂径定理和等腰三角形的性质求得∠BOD=∠A,解直角三角形即可求得sin∠BOD=$\frac{BD}{OB}$=$\frac{2BD}{2R}$=$\frac{BC}{2R}$,从而求得$\frac{BC}{2R}$=sin∠A.
(3)因为AC的最大值是圆的直径,只要求得△ABC外接圆的直径即可,根据(2)结论即可求得.
解答 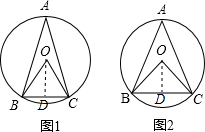 解:(1)如图1,∵∠A=30°,
解:(1)如图1,∵∠A=30°,
∴∠BOC=60°,
作OD⊥BC于D,
∴BD=DC,
∴OB=OC,
∴∠BOD=∠COD=$\frac{1}{2}$∠BOC=30°,
∴sin∠BOD=$\frac{BD}{OB}$=$\frac{1}{2}$,
∴$\frac{2BD}{2OB}$=$\frac{1}{2}$,
即$\frac{BC}{2R}$=$\frac{1}{2}$;
如图2,∵∠A=45°,
∴∠BOC=90°,
作OD⊥BC于D,
∴BD=DC,
∴OB=OC,
∴∠BOD=∠COD=$\frac{1}{2}$∠BOC=45°,
∴sin∠BOD=$\frac{BD}{OB}$=$\frac{\sqrt{2}}{2}$,
∴$\frac{2BD}{2OB}$=$\frac{\sqrt{2}}{2}$
即$\frac{BC}{2R}$=$\frac{\sqrt{2}}{2}$
故答案为$\frac{1}{2}$,$\frac{\sqrt{2}}{2}$;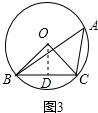
(2)猜想:$\frac{BC}{2R}$=sin∠A;
如图3,作OD⊥BC于D,
∴BD=CD,
∵OB=OC,
∴$∠BOD=\frac{1}{2}$∠BOC,
∵∠BOC=2∠A,
∴∠BOD=∠A,
在RT△BOD中,sin∠BOD=$\frac{BD}{OB}$=$\frac{2BD}{2R}$=$\frac{BC}{2R}$,
∴$\frac{BC}{2R}$=sin∠A.
故答案为sin∠A.
(3)当AC是外接圆的直径时,AC最大,
由(2)可知sin∠A=$\frac{BC}{2R}$,
∵∠A=60°,BC=4,
∴2R=$\frac{BC}{sin60°}$=$\frac{4}{\frac{\sqrt{3}}{3}}$=4$\sqrt{3}$.
即AC的最大值为4$\sqrt{3}$.
点评 本题考查了圆周角定理以及直角三角形的正弦函数,作出辅助线构建直角三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
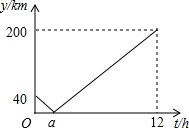 甲、乙两车要从M地沿同一条公路运输一批物资到N地,乙车比甲车先行驶1h,设甲车与乙车之间的距离为y(单位:km),甲车行驶时间为t(单位:h),y与t之间的函数关系如图所示(假设甲、乙两车速度始终保持不变).结合图象解答下列问题:
甲、乙两车要从M地沿同一条公路运输一批物资到N地,乙车比甲车先行驶1h,设甲车与乙车之间的距离为y(单位:km),甲车行驶时间为t(单位:h),y与t之间的函数关系如图所示(假设甲、乙两车速度始终保持不变).结合图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB=A′B′,BC=B′C′,∠C=∠C′ | |
| B. | ∠B=135°,∠B′=135°,AB=B′C′,BC=C′A′ | |
| C. | AB=BC=CA,A′B′=B′C′=C′A′,∠A=∠A′ | |
| D. | AB=A′B′,BC=B′C′,∠B=∠B′=135° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com