
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx+3经过点N(2,-5),过点N作x轴的平行线交此抛物线左侧于点M,MN=6.
(1)求此抛物线的解析式;
(2)点P(x,y)为此抛物线上一动点,连接MP交此抛物线的对称轴于点D,当△DMN为直角三角形时,求点P的坐标;
(3)设此抛物线与y轴交于点C,在此抛物线上是否存在点Q,使∠QMN=∠CNM?若存在,求出点Q的坐标;若不存在,说明理由.
【答案】(1) y=-x2-2x+3.(2) 点P的坐标为(1,0)或(3,-12).(3) 存在点Q,使∠QMN=∠CNM,点Q的坐标为(-2,3)或(6,-45).
【解析】
试题分析:(1)根据MN平行x轴,MN=6,点N坐标为(2,-5),可得出点M的坐标,然后利用待定系数法求解函数解析式即可;
(2)设抛物线的对称轴x=-1交MN于点G,此时抛物线的对称轴是MN的中垂线,根据△DMN为直角三角形,可得出D1及D2的坐标,分别求出MD1及MD2的函数解析式,结合抛物线可得出点P的坐标;
(3)分两种情况进行讨论,①点Q在MN上方,②点Q在MN下方,然后根据两角相等,利用三角函数建立方程,解出x的值后检验即可得出答案.
试题解析:(1)由题意得,MN平行x轴,MN=6,点N坐标为(2,-5),
故可得点M坐标为(-4,-5),
∵y=ax2+bx+3过点M(-4,-5)、N(2,-5),
∴可得![]() ,
,
解得:![]() ,
,
故此抛物线的解析式为y=-x2-2x+3.
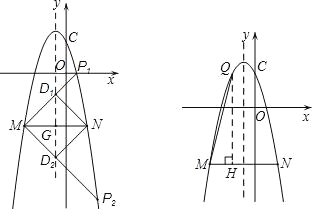
(2)设抛物线的对称轴x=-1交MN于点G,
若△DMN为直角三角形,则![]() ,
,
可得D1(-1,-2),D2(-1,-8),
从而可求得直线MD1解析式为;y=x-1,直线MD2解析式为:y=-x-9,
将P(x,-x2-2x+3)分别代入直线MD1,MD2的解析式,
得-x2-2x+3=x-1①,-x2-2x+3=-x-9②、
解①得 x1=1,x2=-4(舍),
即P1(1,0);
解②得 x3=3,x4=-4(舍),
即P2(3,-12);
故当△DMN为直角三角形时,点P的坐标为(1,0)或(3,-12).
(3)设存在点Q(x,-x2-2x+3),使得∠QMN=∠CNM,
①若点Q在MN上方,过点Q作QH⊥MN,交MN于点H,
则QH=-x2-2x+3+5,MH=(x+4)、
故![]() ,即-x2-2x+3+5=4(x+4)、
,即-x2-2x+3+5=4(x+4)、
解得x1=-2,x2=-4(舍),
故可得点Q1(-2,3);
②若点Q在MN下方,
同理可得Q2(6,-45).
综上可得存在点Q,使∠QMN=∠CNM,点Q的坐标为(-2,3)或(6,-45).


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】如图,已知BD是矩形ABCD的对角线.

(1)用直尺和圆规作线段BD的垂直平分线,分别交AD、BC于E、F(保留作图痕迹,不写作法和证明).
(2)连结BE,DF,问四边形BEDF是什么四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市政府建设一项水利工程,某运输公司承担运送总量为106m3的土石方任务,该公司有甲、乙两种型号的卡车共100辆,甲型车平均每天可以运送土石方80m3,乙型车平均每天可以运送土石方120m3,计划100天完成运输任务.
(1)该公司甲、乙两种型号的卡车各有多少台?
(2)如果该公司用原有的100辆卡车工作了40天后,由于工程进度的需要,剩下的所有运输任务必须在50天内完成,在甲型卡车数量不变情况下,公司至少应增加多少辆乙型卡车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学在创建绿色和谐校园活动中要在一块三角形花圃里种植两种不同的花草,同时拟从A点修建一条花间小径到边BC。
(1)若要使修建小路所使用的材料最少,请在图中画出小路AD,你的理由是 。
(2) 将如图方格中的图形向右平移4格,再向上平移2格,在方格中画出平移后的图形.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com