
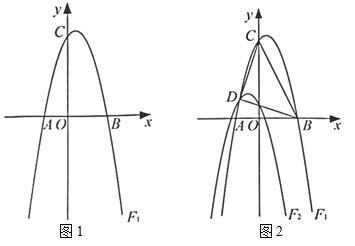
【题目】如图1所示,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线![]() 的表达式;
的表达式;
(2)如图2,将抛物线![]() 先向左平移1个单位,再向下平移3个单位,得到抛物线
先向左平移1个单位,再向下平移3个单位,得到抛物线![]() ,若抛物线
,若抛物线![]() 与抛物线
与抛物线![]() 相交于点
相交于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
①求点![]() 的坐标;
的坐标;
②判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)在(2)的条件下,抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 为等腰直角三角形,若存在,求出点
为等腰直角三角形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)①点
;(2)①点![]() 的坐标
的坐标![]() ;②
;②![]() 是等腰直角三角形,理由见解析;(3)
是等腰直角三角形,理由见解析;(3)![]() 或
或![]() .
.
【解析】
(1)将点![]() 代入即可得;
代入即可得;
(2)①先根据二次函数的平移规律得出抛物线![]() 的表达式,再联立两条抛物线的表达式求解即可得;
的表达式,再联立两条抛物线的表达式求解即可得;
②先根据抛物线![]() 的表达式求出点B、C的坐标,再利用两点之间的距离公式分别求出BC、BD、CD的长,然后根据勾股定理的逆定理、等腰三角形的定义即可得;
的表达式求出点B、C的坐标,再利用两点之间的距离公式分别求出BC、BD、CD的长,然后根据勾股定理的逆定理、等腰三角形的定义即可得;
(3)设点P的坐标为![]() ,根据等腰直角三角形的定义分三种情况:①当
,根据等腰直角三角形的定义分三种情况:①当![]() 时,先根据等腰直角三角形的性质、线段中点的点坐标求出点P的坐标,再代入抛物线
时,先根据等腰直角三角形的性质、线段中点的点坐标求出点P的坐标,再代入抛物线![]() 的表达式,检验点P是否在抛物线
的表达式,检验点P是否在抛物线![]() 的表达式上即可;②当
的表达式上即可;②当![]() 时,先根据平行四边形的判定得出四边形BCDP是平行四边形,再根据点C至点B的平移方式与点D至点P的平移方式相同可求出点P的坐标,然后代入抛物线
时,先根据平行四边形的判定得出四边形BCDP是平行四边形,再根据点C至点B的平移方式与点D至点P的平移方式相同可求出点P的坐标,然后代入抛物线![]() 的表达式,检验点P是否在抛物线
的表达式,检验点P是否在抛物线![]() 的表达式上即可;③当
的表达式上即可;③当![]() 时,先根据等腰直角三角形的性质得出点P在在线段BD的垂直平分线上,再利用待定系数法求出BD的垂直平分线上所在直线的解析式,然后根据两点之间的距离公式和
时,先根据等腰直角三角形的性质得出点P在在线段BD的垂直平分线上,再利用待定系数法求出BD的垂直平分线上所在直线的解析式,然后根据两点之间的距离公式和![]() 可求出点P的坐标,最后代入抛物线
可求出点P的坐标,最后代入抛物线![]() 的表达式,检验点P是否在抛物线
的表达式,检验点P是否在抛物线![]() 的表达式上即可.
的表达式上即可.
(1)将点![]() 代入抛物线
代入抛物线![]() 的表达式得:
的表达式得:![]()
解得![]()
则抛物线![]() 的表达式为
的表达式为![]()
故抛物线![]() 的表达式为
的表达式为![]() ;
;
(2)①由二次函数的平移规律得:抛物线![]() 的表达式为
的表达式为![]()
即![]()
联立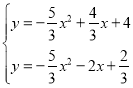 ,解得
,解得![]()
则点![]() 的坐标为
的坐标为![]() ;
;
②对于![]()
当![]() 时,
时,![]() ,解得
,解得![]() 或
或![]()
则点B的坐标为![]()
当![]() 时,
时,![]() ,则点C的坐标为
,则点C的坐标为![]()
由两点之间的距离公式得:![]()
![]()
![]()
则![]() ,
,![]()
故![]() 是等腰直角三角形;
是等腰直角三角形;
(3)抛物线![]() 的表达式为
的表达式为![]()
设点P的坐标为![]()
由题意,分以下三种情况:
①当![]() 时,
时,![]() 为等腰直角三角形
为等腰直角三角形
![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]()
![]()
![]()
![]() 点D是CP的中点
点D是CP的中点
则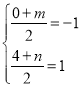 ,解得
,解得![]()
即点P的坐标为![]()
对于抛物线![]() 的表达式
的表达式![]()
当![]() 时,
时,![]()
即点![]() 在抛物线
在抛物线![]() 上,符合题意
上,符合题意
②当![]() 时,
时,![]() 为等腰直角三角形
为等腰直角三角形
![]() ,
,![]()
![]() ,
,![]()
![]() 四边形BCDP是平行四边形
四边形BCDP是平行四边形
![]() 点C至点B的平移方式与点D至点P的平移方式相同
点C至点B的平移方式与点D至点P的平移方式相同
![]()
![]() 点C至点B的平移方式为先向下平移4个单位长度,再向右平移2个单位长度
点C至点B的平移方式为先向下平移4个单位长度,再向右平移2个单位长度
![]()
![]()
即点P的坐标为![]()
对于抛物线![]() 的表达式
的表达式![]()
当![]() 时,
时,![]()
即点![]() 在抛物线
在抛物线![]() 上,符合题意
上,符合题意
③当![]() 时,
时,![]() 为等腰直角三角形
为等腰直角三角形
则点P在线段BD的垂直平分线上
设直线BD的解析式![]()
将点![]() 代入得:
代入得:![]() ,解得
,解得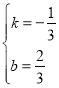
则直线BD的解析式![]()
设BD的垂线平分线所在直线的解析式为![]()
点![]() 的中点的坐标为
的中点的坐标为![]() ,即
,即![]()
将点![]() 代入
代入![]() 得:
得:![]() ,解得
,解得![]()
则BD的垂线平分线所在直线的解析式为![]()
因此有![]() ,即点P的坐标为
,即点P的坐标为![]()
由两点之间的距离公式得:![]()
又![]() ,
,![]() 为等腰直角三角形
为等腰直角三角形
![]()
则![]()
解得![]() 或
或![]()
当![]() 时,
时,![]() ,即点P的坐标为
,即点P的坐标为![]()
当![]() 时,
时,![]() ,即点P的坐标为
,即点P的坐标为![]()
对于抛物线![]() 的表达式
的表达式![]()
当![]() 时,
时,![]()
即点![]() 不在抛物线
不在抛物线![]() 上,不符合题意,舍去
上,不符合题意,舍去
当![]() 时,
时,![]()
即点![]() 不在抛物线
不在抛物线![]() 上,不符合题意,舍去
上,不符合题意,舍去
综上,符合条件的点P的坐标为![]() 或
或![]() .
.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中只装有2个白色围棋子和1个黑色围棋子,围棋子除颜色外其余均相同.从这个盒子中随机地摸出1个围棋子,记下颜色后放回,搅匀后再随机地摸出1个围棋子记下颜色.请用画树状图(或列表)的方法,求两次摸出的围棋子颜色都是白色的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年2月,贵州省积极响应国家“停课不停学”的号召,推出了“空中黔课”.为了解某中学初三学生每天听空中黔课的时间,随机调查了该校部分初三学生.根据调查结果,绘制出了如下统计图表(不完整),请根据相关信息,解答下列问题:
部分初三学生每天听空中黔课时间的人数统计表
时间/ | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
人数/人 | 2 | 6 | 6 | 10 |
| 4 |
部分初三学生每天听空中黔课时间的人数统计图
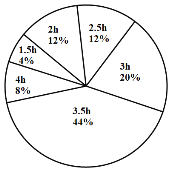
(1)本次共调查的学生人数为_____,在表格中,![]() ___;
___;
(2)统计的这组数据中,每天听空中黔课时间的中位数是____,众数是_____;
(3)请就疫情期间如何学习的问题写出一条你的看法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数y=x2+2mx+2n,交x轴于A,B两点(A在B的左侧)
(1)当m=3时,n=4时, ①求A、B两点坐标;②将抛物线向右平移k个单位后交x轴于M、N(M在N的左侧),若B、M三等分AN,直接写出k的值;
(2)当m=1时,若线段AB上有且只有5个点的横坐标为整数,求n的取值范围;
(3)记A(x1,0)、B(x2,0),当m、n都是奇数时,x1、x2能否是有理数?若能,请举例验证,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如表是一个4×4(4行4列共16个“数”组成)的奇妙方阵,从这个方阵中选四个“数”,而且这四个“数”中的任何两个不在同一行,也不在同一列,有很多选法,把每次选出的四个“数”相加,其和是定值,则方阵中第三行三列的“数”是( )
30 |
| 2 | 22 |
﹣3 | ﹣2 | ﹣ | 0 |
|﹣5| | 6 | 23 | |
( | 4 |
| ( |
A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系![]() 中,等腰
中,等腰![]() 的底边
的底边![]() 在
在![]() 轴上,
轴上,![]() ,顶点
,顶点![]() 在
在![]() 的正半轴上,
的正半轴上,![]() ,一动点
,一动点![]() 从
从![]() 出发,以每秒1个单位的速度沿
出发,以每秒1个单位的速度沿![]() 向左运动,到达
向左运动,到达![]() 的中点停止.另一动点
的中点停止.另一动点![]() 从点
从点![]() 出发,以相同的速度沿
出发,以相同的速度沿![]() 向左运动,到达点
向左运动,到达点![]() 停止.已知点
停止.已知点![]() 、
、![]() 同时出发,以
同时出发,以![]() 为边作正方形
为边作正方形![]() ,使正方形
,使正方形![]() 和
和![]() 在
在![]() 的同侧.设运动的时间为
的同侧.设运动的时间为![]() 秒(
秒(![]() ).
).
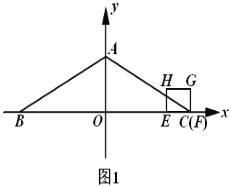
(1)当点![]() 落在
落在![]() 边上时,求
边上时,求![]() 的值;
的值;
(2)设正方形![]() 与
与![]() 重叠面积为
重叠面积为![]() ,请问是存在
,请问是存在![]() 值,使得
值,使得![]() ?若存在,求出
?若存在,求出![]() 值;若不存在,请说明理由;
值;若不存在,请说明理由;
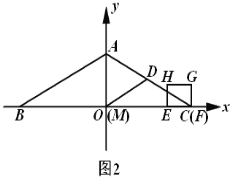
(3)如图2,取![]() 的中点
的中点![]() ,连结
,连结![]() ,当点
,当点![]() 、
、![]() 开始运动时,点
开始运动时,点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位的速度沿
个单位的速度沿![]() 运动,到达点
运动,到达点![]() 停止运动.请问在点
停止运动.请问在点![]() 的整个运动过程中,点
的整个运动过程中,点![]() 可能在正方形
可能在正方形![]() 内(含边界)吗?如果可能,求出点
内(含边界)吗?如果可能,求出点![]() 在正方形
在正方形![]() 内(含边界)的时长;若不可能,请说明理由.
内(含边界)的时长;若不可能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
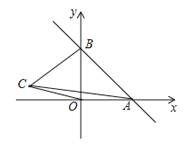
【题目】如图,一次函数y=kx+b的图象分别与x轴,y轴的正半轴分別交于点A,B,AB=2![]() ,∠OAB=45°
,∠OAB=45°
(1)求一次函数的解析式;
(2)如果在第二象限内有一点C(a,![]() );试用含有a的代数式表示四边形ABCO的面积,并求出当△ABC的面积与△ABO的面积相等时a的值;
);试用含有a的代数式表示四边形ABCO的面积,并求出当△ABC的面积与△ABO的面积相等时a的值;
(3)在x轴上,是否存在点P,使△PAB为等腰三角形?若存在,请直接写出所有符合条件的点P坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.
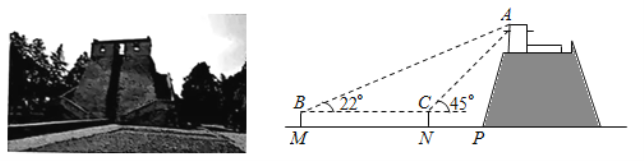
某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水 平步道![]() 上架设测角仪,先在点
上架设测角仪,先在点![]() 处测得观星台最高点
处测得观星台最高点![]() 的仰角为
的仰角为![]() ,然后沿
,然后沿![]() 方向前进
方向前进![]() 到达点
到达点![]() 处,测得点
处,测得点![]() 的仰角为
的仰角为![]() .测角仪的高度为
.测角仪的高度为![]() ,
,
![]() 求观星台最高点
求观星台最高点![]() 距离地面的高度(结果精确到
距离地面的高度(结果精确到![]() .参考数据:
.参考数据: ![]() );
);
![]() “景点简介”显示,观星台的高度为
“景点简介”显示,观星台的高度为![]() ,请计算本次测量结果的误差,并提出一条减小误差的合理化建议.
,请计算本次测量结果的误差,并提出一条减小误差的合理化建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com