
 »зЌЉ£ђЋƒ±я–ќABCD «∆љ––Ћƒ±я–ќ£ђµгPі”Aµг≥цЈҐ£ђ—ЎAD-DC-CB‘»Ћў‘Ћґѓ£ђ‘ЋґѓЋўґ»ќ™1је√„/√л£ђµ±‘Ћґѓ ±Љдќ™0√л°Ђ8√л ±£ђ°чPABµƒ√жїэ÷рљ•‘ціу£їµ±‘Ћґѓ ±Љдќ™8√л°Ђ18√л ±£ђ°чPABµƒ√жїэЇгќ™30£їµ±‘Ћґѓ ±Љдќ™18√л°Ђ26√л ±£ђ°чPABµƒ√жїэ÷рљ•Љх–°£Ѓ
»зЌЉ£ђЋƒ±я–ќABCD «∆љ––Ћƒ±я–ќ£ђµгPі”Aµг≥цЈҐ£ђ—ЎAD-DC-CB‘»Ћў‘Ћґѓ£ђ‘ЋґѓЋўґ»ќ™1је√„/√л£ђµ±‘Ћґѓ ±Љдќ™0√л°Ђ8√л ±£ђ°чPABµƒ√жїэ÷рљ•‘ціу£їµ±‘Ћґѓ ±Љдќ™8√л°Ђ18√л ±£ђ°чPABµƒ√жїэЇгќ™30£їµ±‘Ћґѓ ±Љдќ™18√л°Ђ26√л ±£ђ°чPABµƒ√жїэ÷рљ•Љх–°£ЃЈ÷ќц £®1£©ЄщЊЁћв“вµ√≥цAD=BC=8£ђAB=CD=10£ђµ√≥ц∆љ––Ћƒ±я–ќABCDµƒ√жїэ=60£ђ∆љ––Ћƒ±я–ќABCDµƒ÷№≥§=2£®AB+BC£©=36£ї
£®2£©…и‘Ћґѓ ±Љдќ™t√л£ђЈ÷Ѕљ÷÷«йњц£ЇҐўµ±8£Љt£Љ18 ±£ђ”…»эљ«–ќµƒ√жїэєЎѕµµ√≥цPM£ЇAM=2£Ї3£ђ”…∆љ––Ћƒ±я–ќµƒ–‘÷ µ√≥ц°чPDM°„°чABM£ђµ√≥цґ‘”¶±я≥…±»јэ«у≥цPD=$\frac{2}{3}$AB=$\frac{20}{3}$£ђ«у≥цAD+PD=$\frac{44}{3}$£ђЉіњ…µ√≥цљбєы£ї
ҐЏµ±18£Љt£Љ24 ±£ђ”…»эљ«–ќµƒ√жїэµ√≥цPM£ЇAM=2£Ї3£ђ”…∆љ––Ћƒ±я–ќµƒ–‘÷ µ√≥ц°чPBM°„°чADM£ђµ√≥цґ‘”¶±я≥…±»јэ«у≥цPB=$\frac{2}{3}$AD=$\frac{16}{3}$£ђµ√≥цCP=BC-PB=$\frac{8}{3}$£ђ«у≥цAD+CD+CP=$\frac{62}{3}$£ђЉіњ…µ√≥цљбєы£Ѓ
љвір љв£Ї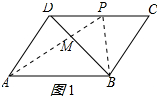 £®1£©ЄщЊЁћв“вµ√£ЇAD=BC=8£ђAB=CD=10£ђ
£®1£©ЄщЊЁћв“вµ√£ЇAD=BC=8£ђAB=CD=10£ђ
°а∆љ––Ћƒ±я–ќABCDµƒ√жїэ=2°Ѕ30=60£ђ∆љ––Ћƒ±я–ќABCDµƒ÷№≥§=2£®AB+BC£©=2°Ѕ18=36£ї
£®2£©…и‘Ћґѓ ±Љдќ™t√л£ђЈ÷Ѕљ÷÷«йњц£Ї
Ґўµ±8£Љt£Љ18 ±£ђ»зЌЉ1Ћщ Њ£Ї
°я°чPBMµƒ√жїэ£Ї°чABMµƒ√жїэ=2£Ї3£ђ
°аPM£ЇAM=2£Ї3£ђ
°яЋƒ±я–ќABCD «∆љ––Ћƒ±я–ќ£ђ
°аAB°ќCD£ђ
°а°чPDM°„°чABM£ђ
°а$\frac{PD}{AB}$=$\frac{PM}{AM}$=$\frac{2}{3}$£ђ
°аPD=$\frac{2}{3}$AB=$\frac{20}{3}$£ђ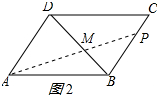
°аAD+PD=8+$\frac{20}{3}$=$\frac{44}{3}$£ђ
°аt=$\frac{44}{3}$°¬1=$\frac{44}{3}$£®s£©£ї
ҐЏµ±18£Љt£Љ24 ±£ђ»зЌЉ2Ћщ Њ£Ї
°я°чPBMµƒ√жїэ£Ї°чABMµƒ√жїэ=2£Ї3£ђ
°аPM£ЇAM=2£Ї3£ђ
°яЋƒ±я–ќABCD «∆љ––Ћƒ±я–ќ£ђ
°аAD°ќBC£ђ
°а°чPBM°„°чADM£ђ
°а$\frac{PB}{AD}=\frac{PM}{AM}$=$\frac{2}{3}$£ђ
°аPB=$\frac{2}{3}$AD=$\frac{16}{3}$£ђ
°аCP=BC-PB=8-$\frac{16}{3}$=$\frac{8}{3}$£ђ
°аAD+CD+CP=8+10+$\frac{8}{3}$=$\frac{62}{3}$£ђ
°аt=$\frac{62}{3}$°¬1=$\frac{62}{3}$£®s£©£ї
„џ…ѕЋщ ц£Їµ±°чPBMµƒ√жїэ”л°чABMµƒ√жїэ±»ќ™2£Ї3 ±£ђµгPµƒ‘Ћґѓ ±Љдќ™$\frac{44}{3}$sїт$\frac{62}{3}$s£Ѓ
µг∆ј ±ЊћвњЉ≤йЅЋ∆љ––Ћƒ±я–ќµƒ–‘÷ °ҐѕаЋ∆»эљ«–ќµƒ∆љ––”Џ–‘÷ °Ґ»эљ«–ќµƒ√жїэєЎѕµ£ї мЅЈ’∆ќ’∆љ––Ћƒ±я–ќµƒ–‘÷ £ђ÷§√ч»эљ«–ќѕаЋ∆ «љвЊцќ ћвµƒєЎЉь£Ѓ



| ƒкЉґ | Єя÷–њќ≥ћ | ƒкЉґ | ≥х÷–њќ≥ћ |
| Єя“ї | Єя“ї√вЈ—њќ≥ћЌ∆Љц£° | ≥х“ї | ≥х“ї√вЈ—њќ≥ћЌ∆Љц£° |
| Єяґю | Єяґю√вЈ—њќ≥ћЌ∆Љц£° | ≥хґю | ≥хґю√вЈ—њќ≥ћЌ∆Љц£° |
| Єя»э | Єя»э√вЈ—њќ≥ћЌ∆Љц£° | ≥х»э | ≥х»э√вЈ—њќ≥ћЌ∆Љц£° |
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї—°‘сћв
| A£Ѓ | 2£®x+y£©£®x-y£© | B£Ѓ | 4£®x+y£©£®x-y£© | C£Ѓ | £®x+y£©£®x-y£© | D£Ѓ | 4£®x+y£©2 |
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї—°‘сћв
 »зЌЉ£ђ‘Џ∆љ––Ћƒ±я–ќABCD÷–£ђAD=5£ђAB=3£ђAE∆љЈ÷°ѕBADљїBC±я”ЏµгE£ђ‘тѕяґќECµƒ≥§ґ» «£®°°°°£©
»зЌЉ£ђ‘Џ∆љ––Ћƒ±я–ќABCD÷–£ђAD=5£ђAB=3£ђAE∆љЈ÷°ѕBADљїBC±я”ЏµгE£ђ‘тѕяґќECµƒ≥§ґ» «£®°°°°£©| A£Ѓ | 4 | B£Ѓ | 3 | C£Ѓ | 2 | D£Ѓ | 1 |
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Їљвірћв

≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Їћоњ’ћв
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Їћоњ’ћв
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї—°‘сћв
| …нЄя£®m£© | 1.50 | 1.54 | 1.58 | 1.62 | 1.66 | 1.70 |
| »Ћ э | 2 | 3 | 5 | 4 | 5 | 1 |
| A£Ѓ | 1.54 | B£Ѓ | 1.58 | C£Ѓ | 1.60 | D£Ѓ | 1.62 |
≤йњіір∞ЄЇЌљвќц>>
њ∆ƒњ£Ї≥х÷– э—І јі‘і£Ї ћв–Ќ£Ї—°‘сћв
| A£Ѓ | ’вЄцќ ћв | B£Ѓ | ’в÷І± «ЇЏ…Ђµƒ | C£Ѓ | “їґ®ѕаµ» | D£Ѓ | ї≠“їћхѕяґќ |
≤йњіір∞ЄЇЌљвќц>>
єъЉ —І–£”≈—° - ЅЈѕ∞≤бЅ–±н - ‘ћвЅ–±н
Їю±± °ї•Ѕ™Ќшќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®∆љћ® | Ќш…ѕ”–Ї¶–≈ѕҐЊў±®„®«ш | µз–≈’©∆≠Њў±®„®«ш | …жјъ Ј–йќё÷ч“е”–Ї¶–≈ѕҐЊў±®„®«ш | …ж∆у«÷»®Њў±®„®«ш
ќ•Ј®ЇЌ≤їЅЉ–≈ѕҐЊў±®µзї∞£Ї027-86699610 Њў±®” ѕд£Ї58377363@163.com