
【题目】问题背景:
(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 .
探索延伸:
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF= ![]() ∠BAD,上述结论是否仍然成立,并说明理由.
∠BAD,上述结论是否仍然成立,并说明理由. 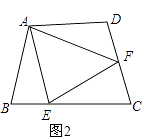
【答案】
(1)EF=BE+DF
(2)证明:结论EF=BE+DF仍然成立;
理由:延长FD到点G.使DG=BE.连结AG,
在△ABE和△ADG中,
 ,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF= ![]() ∠BAD,
∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
 ,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF
【解析】证明:(1)在△ABE和△ADG中,  ,
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF= ![]() ∠BAD,
∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中, ,
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
故答案为 EF=BE+DF.
(1)延长FD到点G.使DG=BE.连结AG,即可证明△ABE≌△ADG,可得AE=AG,再证明△AEF≌△AGF,可得EF=FG,即可解题;(2)延长FD到点G.使DG=BE.连结AG,即可证明△ABE≌△ADG,可得AE=AG,再证明△AEF≌△AGF,可得EF=FG,即可解题.


科目:初中数学 来源: 题型:
【题目】南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向东南方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后在C处成功拦截不明船只,问我国海监执法船在前往监视巡查的过程中行驶了多少海里?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为( )

A.100米 B.99米 C.98米 D.74米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com