
【题目】如图在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A、D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
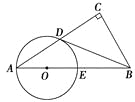
(1)求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径.
【答案】解:(1)证明:连接OD,
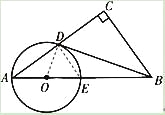
∵OA=OD,
∴∠A=∠ADO,
又∵∠A+∠CDB=90°,
∴∠ADO+∠CDB=90°,
∴∠ODB=180°﹣(∠ADO+∠CDB)=90°,
∴BD⊥OD,
∴BD是⊙O切线;
(2)连接DE,
∵AE是直径,
∴∠ADE=90°,
又∵∠C=90°,
∴∠ADE=∠C,
∴DE∥BC,
又∵D是AC中点,
∴AD=CD,
∴AD:CD=AE:BE,
∴AE=BE,
∵DE∥BC,
∴△ADE∽△ACB,
∴AD:AE=AC:AB,
∴AC:AB=4:5,
设AC=4x,AB=5x,那么BC=3x,
∴BC:AB=3:5,
∵BC=6,
∴AB=10,
∴AE=![]() AB=10.
AB=10.
【解析】试题分析:(1)、连接OD,根据△AOD为等腰三角形可得∠A=∠ODA,根据∠A+∠CDB=90°可得∠ODA+∠CDB=90°,从而得出∠BDO=90°;(2)、连接OE,根据直径所对的圆周角为直角得出∠ADE=90°,根据D为中点可得E为AB的中点,根据△ADE和△ACB相似可得AC:AB=4:5,然后求出BC的长度,从而得出直径的长度.
试题解析:(1)、连接OD,在△AOD中,OA=OD, ∴∠A=∠ODA,
又∵∠A+∠CDB=90° ∴∠ODA+∠CDB=90°, ∴∠BDO=180°-90°=90°,即OD⊥BD,
∴BD与⊙O相切.
(2)、连接DE,∵AE是⊙O的直径, ∴∠ADE=90°, ∴DE∥BC.
又∵D是AC的中点,∴AE=BE. ∴△AED∽△ABC.
∴AC∶AB=AD∶AE. ∵AD:AE=4:5 ∴AC∶AB=4∶5,
令AC=4x,AB=5x,则BC=3x. ∵BC=6,∴AB=10,
∴AE=5,∴⊙O的直径为5.


科目:初中数学 来源: 题型:
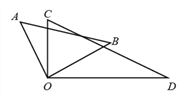
【题目】如图,将一副三角尺的直角顶点重合在一起.
(1)若 OB 是∠DOC 的角平分线,求∠AOD 的补角的度数是多少?
(2)若 ∠COB 与 ∠DOA 的比是 2:7,求 ∠BOC 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中正确的有( )
①两条对角线相等的四边形是矩形
②有一组邻边相等的平行四边形是菱形
③对角线互相垂直平分的四边形是正方形
④对角线相等且互相平分的四边形是矩形.
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD⊥DC,AB∥DC,AB=BC,AD与BC延长线交于点F,G是DC延长线上一点,AG⊥BC于E,
(1)求证:CF=CG;
(2)连接DE,若BE=4CE,CD=2求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是( )

①∠AOB=∠COD;
②∠AOB+∠COD=90°;
③∠BOC+∠AOD=180°;
④∠AOC-∠COD=∠BOC.
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com