
【题目】如图,矩形ABCD中,AD=4,∠CAB=30°,点P是线段AC上的动点,点Q是线段CD上的动点,则AQ+QP的最小值是 . 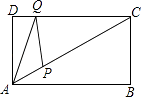
【答案】4 ![]()
【解析】解:以CD为轴,将△ACD往上翻转180°,如图,
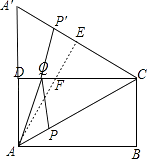
过点A作AE⊥A′C于E点,AE交CD于F点,
当Q与F点重合,P′与E点重合时,AQ+QP=AF+EF=AE最短(直线外一点到这条直线中,垂线段最短),
∵矩形ABCD中,AD=4,∠CAB=30°,
∴∠A′CD=∠ACD=∠CAB=30°,3
∴∠A′CA=60°,
又∵AC=A′C,
∴△A′CA为等边三角形,且A′A=2AD=8,
AE=A′Asin∠A′CA=8× ![]() =4
=4 ![]() .
.
故答案为:4 ![]() .
.
这是一道双动点问题,以CD为轴,将ACD往上翻转180°,由已知矩形ABCD中,∠CAB=30°,可以得到∠A′AC=60°,易证得△A′AC是等边三角形,求出边A′C上的高,由两点之间线段最短即可得出结论。也可以作点A关于点D的中心对称点A′,过点A′作AC的垂线即可。


科目:初中数学 来源: 题型:
【题目】中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽测了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图:
请你根据图中的信息,解答下列问题:
(1)写出扇形图中a=%,并补全条形图;
(2)在这次抽测中,测试成绩的众数和中位数分别是 个、个.
(3)该区体育中考选报引体向上的男生共有1800人,如果体育中考引体向上达6个以上(含6个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
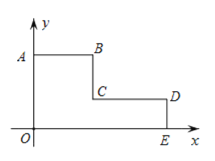
【题目】如图,在平面直角坐标系中,点O,A,B,C,D,E的坐标分别为(0,0)(0,5),(4,5),(4,2),(9,2),(9,0).
(1)求这个图形的周长;
(2)求这个图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂对零件进行检测,引进了检测机器.已知一台检测机的工作效率相当于一名检测员的20倍.若用这台检测机检测900个零件要比15名检测员检测这些零件少3小时.
(1)求一台零件检测机每小时检测零件多少个?
(2)现有一项零件检测任务,要求不超过7小时检测完成3450个零件.该厂调配了2台检测机和30名检测员,工作3小时后又调配了一些检测机进行支援,则该厂至少再调配几台检测机才能完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC为边长为6的等边三角形,D,E分别在边BC,AC上,且CD=CE=x,连接DE并延长至点F,使EF=AE,连接AF,CF.
(1)求证:△AEF为等边三角形;
(2)求证:四边形ABDF是平行四边形;
(3)记△CEF的面积为S,
①求S与x的函数关系式;
②当S有最大值时,判断CF与BC的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数码专营店销售甲、乙两种品牌智能手机,这两种手机的进价和售价如下表所示:
甲 | 乙 | |
进价(元/部) | 4300 | 3600 |
售价(元/部) | 4800 | 4200 |
(1)该店销售记录显示.三月份销售甲、乙两种手机共17部,且销售甲种手机的利润恰好是销售乙种手机利润的2倍,求该店三月份售出甲种手机和乙种手机各多少部?
(2)根据市场调研,该店四月份计划购进这两种手机共20部,要求购进乙种手机数不超过甲种手机数的![]() ,而用于购买这两种手机的资金低于81500元,请通过计算设计所有可能的进货方案.
,而用于购买这两种手机的资金低于81500元,请通过计算设计所有可能的进货方案.
(3)在(2)的条件下,该店打算将四月份按计划购进的20部手机全部售出后,所获得利润的30%用于购买A,B两款教学仪器捐赠给某希望小学.已知购买A仪器每台300元,购买B仪器每台570元,且所捐的钱恰好用完,试问该店捐赠A,B两款仪器一共多少台?(直接写出所有可能的结果即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com