练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    先化简，再求值：÷（1﹣），其中x=0．

    　


    【考点】分式的化简求值．

    【分析】先根据分式混合运算的法则把原式进行化简，再把x=0代入进行计算即可．

    【解答】解：原式=÷（﹣）

    =•

    =，

    当x=0时，原式=．

    【点评】本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．

    　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


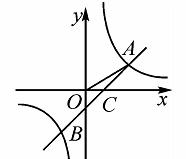
    如图，反比例函数y= 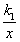与一次函数y=k2x+b图象的交点为4(m，1)，B（-2，n），OA与x轴正方向的夹角为α，且tanα=．

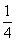      (1)求反比例函数及一次函数的表达式；

      (2)设直线AB与x轴交于点C，且AC与x轴正方向的夹角为β，求tanβ的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某次射击训练中，一小组的成绩如下表所示．若该小组的平均成绩为7.7环，则成绩为8环的人数是　　　　　　．

    环数

    6

    7

    8

    9

    人数

    1

    3

     

    2

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    分式方程的解是（　　）

    A．x=﹣1      B．x=  C．x=﹣3      D．x=

    查看答案和解析>>

    科目：初中数学 来源： 题型：


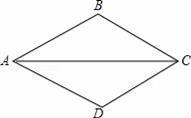
    如图，已知△ABC，按如下步骤作图：①以A为圆心，AB长为半径画弧；②以C为圆心，CB长为半径画弧，两弧相交于点D；③连结AD，CD．则△ABC≌△ADC的依据是　　　　　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    情境观察：

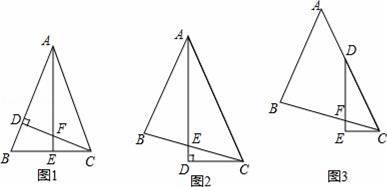
    如图1，△ABC中，AB=AC，∠BAC=45°，CD⊥AB，AE⊥BC，垂足分别为D、E，CD与AE交于点F．

    ①写出图1中所有的全等三角形　　　　　　；

    ②线段AF与线段CE的数量关系是　　　　　　．

    问题探究：

    如图2，△ABC中，∠BAC=45°，AB=BC，AD平分∠BAC，AD⊥CD，垂足为D，AD与BC交于点E．

    求证：AE=2CD．

    拓展延伸：

    如图3，△ABC中，∠BAC=45°，AB=BC，点D在AC上，∠EDC=∠BAC，DE⊥CE，垂足为E，DE与BC交于点F．求证：DF=2CE．

    要求：请你写出辅助线的作法，并在图3中画出辅助线，不需要证明．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列计算正确的是(   )

     A. 92=18      B. －22=4        C. 2×(－2)=(－2)     D. 22＋22=2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    为了加强公民的节水意识，北方某市制定了如下收费标准：每户每月的用水量不超过10吨时，水价每吨3元，超过10吨时,超过的部分按每吨5元收费,小明家九月份用水x吨.

    （1）试用x 的整式表示小明家九月份应该缴纳的收费：

    （2）据预测“十一”黄金周期间，他家外出旅游，该月用水量将比九月份减少4吨，水费减少，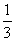

    求x的值。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    解分式方程： =﹣．

    查看答案和解析>>

    同步练习册答案