Question

情境观察：

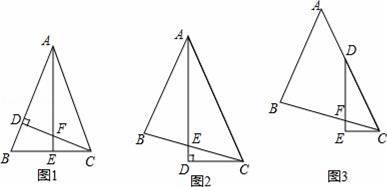
如图1，△ABC中，AB=AC，∠BAC=45°，CD⊥AB，AE⊥BC，垂足分别为D、E，CD与AE交于点F．

①写出图1中所有的全等三角形　　　　　　；

②线段AF与线段CE的数量关系是　　　　　　．

问题探究：

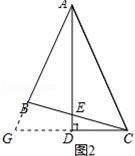
如图2，△ABC中，∠BAC=45°，AB=BC，AD平分∠BAC，AD⊥CD，垂足为D，AD与BC交于点E．

求证：AE=2CD．

拓展延伸：

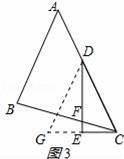
如图3，△ABC中，∠BAC=45°，AB=BC，点D在AC上，∠EDC=∠BAC，DE⊥CE，垂足为E，DE与BC交于点F．求证：DF=2CE．

要求：请你写出辅助线的作法，并在图3中画出辅助线，不需要证明．

　

Answer 1

【考点】全等三角形的判定与性质．

【分析】情境观察：①由全等三角形的判定方法容易得出结果；

②由全等三角形的性质即可得出结论；

问题探究：延长AB、CD交于点G，由ASA证明△ADC≌△ADG，得出对应边相等CD=GD，即CG=2CD，证出∠BAE=∠BCG，由ASA证明△ADC≌△CBG，得出AE=CG=2CD即可．

拓展延伸：作DG⊥BC交CE的延长线于G，同上证明三角形全等，得出DF=CG即可．

【解答】情境观察：

解：①图1中所有的全等三角形为△ABE≌△ACE，△ADF≌△CDB；

故答案为：△ABE≌△ACE，△ADF≌△CDB

②线段AF与线段CE的数量关系是：AF=2CE；

故答案为：AF=2CE．

问题探究：

证明：延长AB、CD交于点G，如图2所示：

∵AD平分∠BAC，

∴∠CAD=∠GAD，

∵AD⊥CD，

∴∠ADC=∠ADG=90°，

在△ADC和△ADG中，

，

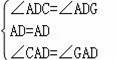
∴△ADC≌△ADG（ASA），

∴CD=GD，即CG=2CD，

∵∠BAC=45°，AB=BC，

∴∠ABC=90°，

∴∠CBG=90°，

∴∠G+∠BCG=90°，

∵∠G+∠BAE=90°，

∴∠BAE=∠BCG，

在△ABE和△CBG中，

，

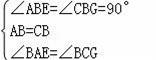
∴△ADC≌△CBG中（ASA），

∴AE=CG=2CD．

拓展延伸：

解：作DG⊥BC交CE的延长线于G，

如图3所示．

【点评】本题考查了全等三角形的判定与性质、等腰三角形的性质等知识；熟练掌握等腰三角形的性质，证明三角形全等是解决问题的关键．