
如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:
(1)△AEF≌△CEB;
(2)AF=2CD.


【考点】全等三角形的判定与性质;等腰三角形的性质.
【专题】证明题.
【分析】(1)由AD⊥BC,CE⊥AB,易得∠AFE=∠B,利用全等三角形的判定得△AEF≌△CEB;
(2)由全等三角形的性质得AF=BC,由等腰三角形的性质“三线合一”得BC=2CD,等量代换得出结论.
【解答】证明:(1)∵AD⊥BC,CE⊥AB,
∴∠BCE+∠CFD=90°,∠BCE+∠B=90°,
∴∠CFD=∠B,
∵∠CFD=∠AFE,
∴∠AFE=∠B
在△AEF与△CEB中,
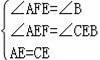
 ,
,
∴△AEF≌△CEB(AAS);
(2)∵AB=AC,AD⊥BC,
∴BC=2CD,
∵△AEF≌△CEB,
∴AF=BC,
∴AF=2CD.
【点评】本题主要考查了全等三角形性质与判定,等腰三角形的性质,运用等腰三角形的性质是解答此题的关键.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
情境观察:
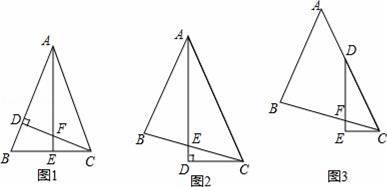

如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.
①写出图1中所有的全等三角形 ;
②线段AF与线段CE的数量关系是 .
问题探究:
如图2,△ABC中,∠BAC=45°,AB=BC,AD平分∠BAC,AD⊥CD,垂足为D,AD与BC交于点E.
求证:AE=2CD.
拓展延伸:
如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC=
 ∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.
∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.
要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
解不等式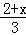 >
>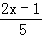 的下列过程中错误的是( )
的下列过程中错误的是( )
A.去分母得5(2+x)>3(2x﹣1) B.去括号得10+5x>6x﹣3
C.移项,合并同类项得﹣x>﹣13 D.系数化为1,得x>13
查看答案和解析>>
科目:初中数学 来源: 题型:
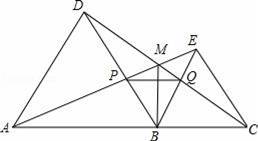
如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,下面结论:
①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④PQ∥AC.
其中结论正确的有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,正方形ABCD的对角线BD长为2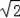
 ,若直线l满足:(1)点D到直线l的距离为1,(2)A、C两点到直线l的距离相等,则符合题意的直线l的条数为( )
,若直线l满足:(1)点D到直线l的距离为1,(2)A、C两点到直线l的距离相等,则符合题意的直线l的条数为( )


A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
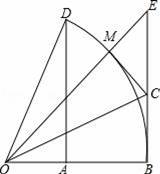
如图,以O为圆心的弧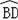
 度数为60°,∠BOE=45°,DA⊥OB,EB⊥OB.
度数为60°,∠BOE=45°,DA⊥OB,EB⊥OB.
(1)求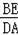
 的值;
的值;
(2)若OE与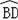
 交于点M,OC平分∠BOE,连接CM.说明CM为⊙O的切线;
交于点M,OC平分∠BOE,连接CM.说明CM为⊙O的切线;
(3)在(2)的条件下,若BC=1,求tan∠BCO的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com