Question

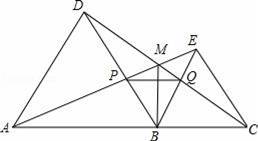
如图，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连接PQ，下面结论：

①△ABE≌△DBC；②∠DMA=60°；③△BPQ为等边三角形；④PQ∥AC．

其中结论正确的有（　　）

A．1个  B．2个   C．3个  D．4个

　

　

Answer 1

D【考点】全等三角形的判定与性质；等边三角形的判定与性质．

【分析】①由等边三角形的性质得出AB=DB，∠ABD=∠CBE=60°，BE=BC，得出∠ABE=∠DBC，由SAS即可证出△ABE≌△DBC；

②由△ABE≌△DBC，得出∠BAE=∠BDC，根据三角形外角的性质得出∠DMA=60°；

③由ASA证明△ABP≌△DBQ，得出对应边相等BP=BQ，即可得出△BPQ为等边三角形；

④推出△BPQ是等边三角形，得到∠PBQ=60°，根据平行线的性质即可得到PQ∥AC，故④正确．

【解答】解：∵△ABD、△BCE为等边三角形，

∴AB=DB，∠ABD=∠CBE=60°，BE=BC，

∴∠ABE=∠DBC，∠PBQ=60°，

在△ABE和△DBC中，

∵，

∴△ABE≌△DBC（SAS），

∴①正确；

∵△ABE≌△DBC，

∴∠BAE=∠BDC，

∵∠BDC+∠BCD=180°﹣60°﹣60°=60°，

∴∠DMA=∠BAE+∠BCD=∠BDC+∠BCD=60°，

∴②正确；

在△ABP和△DBQ中，

∵，

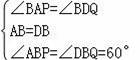
∴△ABP≌△DBQ（ASA），

∴BP=BQ，

∴△BPQ为等边三角形，

∴③正确；

∵BP=BQ，∠PBQ=60°，

∴△BPQ是等边三角形，

∴∠PQB=60°，

∴∠PQB=∠QBC，

∴PQ∥AC，

故④正确．

故选D．

【点评】此题考查了等边三角形的判定与性质与全等三角形的判定与性质，平行线的判定和性质，此题图形比较复杂，解题的关键是仔细识图，找准全等的三角形．