Question

如图，以O为圆心的弧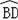度数为60°，∠BOE=45°，DA⊥OB，EB⊥OB．

（1）求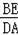的值；

（2）若OE与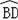交于点M，OC平分∠BOE，连接CM．说明CM为⊙O的切线；

（3）在（2）的条件下，若BC=1，求tan∠BCO的值．

　

Answer 1

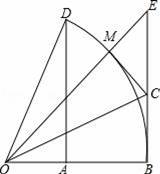
【考点】切线的判定；全等三角形的判定与性质；勾股定理；解直角三角形．

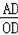
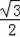
【分析】（1）求出OB=BE，在Rt△OAD中，sin∠AOD==，代入求出即可；

（2）求出∠BOC=∠MOC，证△BOC≌△MOC，推出∠CMO=∠OBC=90°，根据切线的判定推出即可；

（3）求出CM=ME，MC=BC，求出BC=MC=ME=1，在Rt△MCE中，根据勾股定理求出CE=，求出OB=+1，解直角三角形得出tan∠BCO=+1，即可得出答案．

【解答】解：（1）∵EB⊥OB，∠BOE=45°，

∴∠E=45°，

∴∠E=∠BOE，

∴OB=BE，

在Rt△OAD中，sin∠AOD==，

∵OD=OB=BE，

∴==；

 

（2）∵OC平分∠BOE，

∴∠BOC=∠MOC，

在△BOC和△MOC中，

∴△BOC≌△MOC（SAS），

∴∠CMO=∠OBC=90°，

又∵CM过半径OM的外端，

∴CM为⊙O的切线；

 

（3）由（1）（2）证明知∠E=45°，OB=BE，△BOC≌△MOC，CM⊥ME，

∵CM⊥OE，∠E=45°，

∴∠MCE=∠E=45°，

∴CM=ME，

又∵△BOC≌△MOC，

∴MC=BC，

∴BC=MC=ME=1，

∵MC=ME=1，

∴在Rt△MCE中，根据勾股定理，得CE=，

∴OB=BE=+1，

∵tan∠BCO=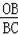，OB=+1，BC=1，

∴tan∠BCO=+1．

【点评】本题考查了切线的性质和判定，全等三角形的性质和判定，勾股定理，切线长定理等知识点的应用，综合性比较强，难度偏大．