
【题目】如图,已知∠1=∠2,∠3=∠E,∠4=∠5,请判断AD与BC的位置关系,并证明你的结论.
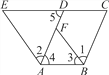
【答案】AD∥BC.理由见解析
【解析】试题分析:首先由内错角∠4=∠5,可证得ED∥AB,所以同旁内角∠E、∠EAB互补,已知∠3=∠E,则∠3、∠EAB互补,由此可证得AE∥BF,即可证得∠2=∠AFB,而∠1=∠2,通过等量代换即可证得∠1=∠AFB,由此可得AD、BC的位置关系是平行.
试题解析:解:结论AD∥BC.证明如下:
∵∠4=∠5(已知),∴EC∥AB(内错角相等,两直线平行),∴∠E+∠EAB=180°(两直线平行,同旁内角互补).
∵∠3=∠E(已知),∴∠3+∠EAB=180°(等量代换),∴AE∥BF(同旁内角互补,两直线平行),∴∠2=∠AFB(两直线平行,内错角相等).
∵∠1=∠2(已知),∴∠1=∠AFB(等量代换),∴AD∥BC(内错角相等,两直线平行).


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】对于实数a,我们规定:用符号[![]() ]表示不大于
]表示不大于![]() 的最大整数,称[
的最大整数,称[![]() ]为a的根整数,例如:[
]为a的根整数,例如:[![]() ]=3,[
]=3,[![]() ]=3.
]=3.
(1)仿照以上方法计算:[![]() ] = ;[
] = ;[![]() ] = .
] = .
(2)若[![]() ]=1,写出满足题意的x的整数值 .
]=1,写出满足题意的x的整数值 .
如果我们对a连续求根整数,直到结果为1为止.例如:对10连续求根整数2次 [![]() ]=3→[
]=3→[![]() ]=1,这时候结果为1.
]=1,这时候结果为1.
(3)对100连续求根整数, 次之后结果为1.
(4)只需进行3次连续求根整数运算后结果为1的所有正整数中,最大的是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师每天坚持晨跑.下图反映的是李老师某天6:20从家出发小跑到赵化北门,在北门休息几分钟后又慢跑回家的函数图象. 其中![]() (分钟)表示所用时间,
(分钟)表示所用时间, ![]() (千米)表示李欢离家的距离.
(千米)表示李欢离家的距离.
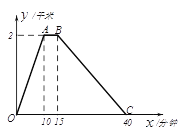
(1)分别求出线段0≤x≤10和15≤x≤40的函数解析式?
(2)李老师在这次晨跑过程中什么时间距离家500米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据宜昌市统计局2013年底统计,中心城区人均住房建筑面积约为30平方米,为把宜昌市建设成特大城市,中心城区住房建筑面积和人口数都迅速增加.2014年中心城区住房建筑面积比2013年中心城区住房建筑面积增长的百分数是a,2015年中心城区住房建筑面积比2013年中心城区住房建筑面积增长的百分数是2a.从2014年开始,中心城区人口数在2013年180万的基础上每年递增m(m>0)万人,这样2015年中心城区的人口数比2014年中心城区人口数的1.5倍少80万人,已知2015年中心城区的人均住房建筑面积与2014年持平.
(1)根据题意填表(用含a,m的式子表示各个数量);
年份 | 中心城区人口数 | 中心城区人均住房建筑面积(单位:平方米) | 中心城区住房建筑面积(单位:万平凡米) |
2013年 | 180 | 30 | 5400 |
2014年 |
|
|
|
2015年 |
|
|
|
(2)求题目中的a和m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个圆锥形和烟囱帽的底面直径是40cm,母线长是120cm,需要加工这样的一个烟囱帽,请你画一画:
(1)至少需要多少厘米铁皮(不计接头)
(2)如果用一张圆形铁皮作为材料来制作这个烟囱帽,那么这个圆形铁皮的半径至少应是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
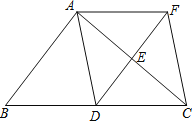
【题目】如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF.
(1)求证:四边形ADCF是平行四边形;
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为建设资源节约型、环境友好型社会,克服因干旱而造成的电力紧张困难,切实做好节能减排工作.某地决定对居民家庭用电实行“阶梯电价”,电力公司规定:居民家庭每月用电量在80千瓦时以下(含80千瓦时,1千瓦时俗称1度)时,实行“基本电价”;当居民家庭月用电量超过80千瓦时时,超过部分实行“提高电价”.
(1)小张家今年2月份用电100千瓦时,上缴电费68元;5月份用电120千瓦时,上缴电费88元.求“基本电价”和“提高电价”分别为多少元/千瓦时;
(2)若6月份小张家预计用电130千瓦时,请预算小张家6月份应上缴的电费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子厂商投产一种新型电子产品,每件制造成本为18元,试销过程中发现,每月销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间的关系可以近似地看作一次函数
(元)之间的关系可以近似地看作一次函数![]() (利润=售价﹣制造成本)
(利润=售价﹣制造成本)
(1)写出每月的利润![]() (万元)与销售单价
(万元)与销售单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)根据相关部门规定,这种电子产品的销售单价不能高于40元,如果厂商每月的制造成本不超过540万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com