
【题目】李老师每天坚持晨跑.下图反映的是李老师某天6:20从家出发小跑到赵化北门,在北门休息几分钟后又慢跑回家的函数图象. 其中![]() (分钟)表示所用时间,
(分钟)表示所用时间, ![]() (千米)表示李欢离家的距离.
(千米)表示李欢离家的距离.
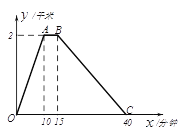
(1)分别求出线段0≤x≤10和15≤x≤40的函数解析式?
(2)李老师在这次晨跑过程中什么时间距离家500米?
【答案】(1)当0≤x≤10时,y=0.1x;当15≤x≤40时,y=3.2-0.08x;
(2)李老师在这次晨跑过程中分别于5分、33.75分距离家500米。
【解析】试题分析:(1)利用待定系数法即可求得;(2)求出OA的解析式,然后根据OA、BC的解析式,利用y=0.5千米计算求出相应的x的值,再加上6点20分即可.
试题解析:(1)设OA的解析式为y1=kx,
则10k=2,
解得k=![]() ,
,
所以,y=![]() x,
x,
设直线BC解析式为y2=k1x+b,
∵函数图象经过点(15,2),(40,0),
∴![]() ,
,
解得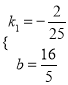 .
.
所以,直线BC解析式为y=![]() x+
x+![]() ;
;
∴线段0x10的函数解析式为y1=![]() x(0x10),
x(0x10),
线段15x40的函数解析式为y2=![]() x+
x+![]() (15x40);
(15x40);
(2)当y1=0.5km时,0.5=![]() x,x=2.5,
x,x=2.5,
当y2=0.5km时,0.5=![]() x+
x+![]() ,x=
,x=![]() =33.75,
=33.75,
∴李老师在这次晨跑过程中分别于6点22.5分和6点53.75分距离家500米。


科目:初中数学 来源: 题型:
【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
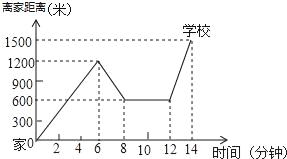
(1)小明家到学校的路程是多少米?
(2)小明在书店停留了多少分钟?
(3)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?
(4)我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列7个事件中:(1)掷一枚硬币,正面朝上.(2)从一副没有大小王的扑克牌中抽出一张恰为黑桃.(3)随意翻开一本有400页的书,正好翻到第100页.(4)天上下雨,马路潮湿.(5)你能长到身高4米.(6)买奖券中特等大奖.(7)掷一枚正方体骰子,得到的点数<7.其中(将序号填入题中的横线上即可)确定事件为________;不确定事件为________;不可能事件为________;必然事件为________;不确定事件中,发生可能性最大的是________,发生可能性最小的是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.
正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°—∠AMN—∠AMB
=180°—∠B—∠AMB
=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正![]() 边形ABCD…X”,请你作出猜想:当∠AMN=°时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
边形ABCD…X”,请你作出猜想:当∠AMN=°时,结论AM=MN仍然成立.(直接写出答案,不需要证明)


图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中, ![]() ,
, ![]() .如图,将
.如图,将![]() 进行折叠,使点
进行折叠,使点![]() 落在线段
落在线段![]() 上(包括点
上(包括点![]() 和点
和点![]() ),设点
),设点![]() 的落点为
的落点为![]() ,折痕为
,折痕为![]() ,当
,当![]() 是等腰三角形时,点
是等腰三角形时,点![]() 可能的位置共有( ).
可能的位置共有( ).
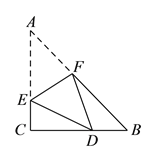
A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:E、F分别是AB和CD上的点,DE、AF分别交BC于点G、H, AB∥CD,∠A=∠D,试说明:(1)AF∥ED;(2)∠BED=∠A;(3) ∠1=∠2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com