
【题目】已知![]() 中,
中, ![]() ,
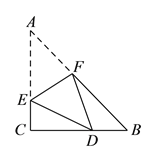
, ![]() .如图,将
.如图,将![]() 进行折叠,使点
进行折叠,使点![]() 落在线段
落在线段![]() 上(包括点
上(包括点![]() 和点
和点![]() ),设点
),设点![]() 的落点为
的落点为![]() ,折痕为
,折痕为![]() ,当
,当![]() 是等腰三角形时,点
是等腰三角形时,点![]() 可能的位置共有( ).
可能的位置共有( ).
A. ![]() 种 B.
种 B. ![]() 种 C.
种 C. ![]() 种 D.
种 D. ![]() 种
种
 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
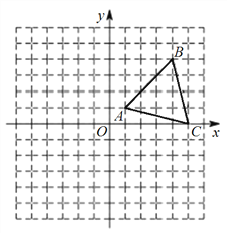
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)写出点B的坐标为________;
(2)将△ABC向左平移5个单位长度,再向下平移3个单位长度,画出平移后得到的△A1B1C1,并直接写出点A1的坐标为________;点C1的坐标为________;
(3)△A1B1C1的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】投掷一枚质地均匀的正方体骰子.
(1)下列说法中正确的有 . (填序号)
①向上一面点数为1点和3点的可能性一样大;
②投掷6次,向上一面点数为1点的一定会出现1次;
③连续投掷2次,向上一面的点数之和不可能等于13.
(2)如果小明连续投掷了10次,其中有3次出现向上一面点数为6点,这时小明说:投掷正方体骰子,向上一面点数为6点的概率是![]() . 你同意他的说法吗?说说你的理由.
. 你同意他的说法吗?说说你的理由.
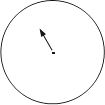
(3)为了估计投掷正方体骰子出现6点朝上的概率,小亮采用转盘来代替骰子做实验.下图是一个可以自由转动的转盘,请你将转盘分为2个扇形区域,分别涂上红、白两种颜色,使得转动转盘,当转盘停止转动后,指针落在红色区域的概率与投掷正方体骰子出现6点朝上的概率相同.(友情提醒:在转盘上用文字注明颜色和扇形圆心角的度数.)
查看答案和解析>>
科目:初中数学 来源: 题型:
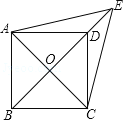
【题目】如图,已知平行四边形ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师每天坚持晨跑.下图反映的是李老师某天6:20从家出发小跑到赵化北门,在北门休息几分钟后又慢跑回家的函数图象. 其中![]() (分钟)表示所用时间,
(分钟)表示所用时间, ![]() (千米)表示李欢离家的距离.
(千米)表示李欢离家的距离.
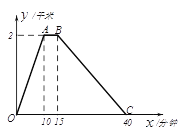
(1)分别求出线段0≤x≤10和15≤x≤40的函数解析式?
(2)李老师在这次晨跑过程中什么时间距离家500米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】母亲节前夕,某淘宝店主从厂家购进A、B两种礼盒,已知A、B两种礼盒的单价比为2:3,单价和为200元.
(1)求A、B两种礼盒的单价分别是多少元?
(2)该店主购进这两种礼盒恰好用去9600元,且购进A种礼盒最多36个,B种礼盒的数量不超过A种礼盒数量的2倍,共有几种进货方案?
(3)根据市场行情,销售一个A种礼盒可获利10元,销售一个B种礼盒可获利18元.为奉献爱心,该店主决定每售出一个B种礼盒,为爱心公益基金捐款m元,每个A种礼盒的利润不变,在(2)的条件下,要使礼盒全部售出后所有方案获利相同,m值是多少?此时店主获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据宜昌市统计局2013年底统计,中心城区人均住房建筑面积约为30平方米,为把宜昌市建设成特大城市,中心城区住房建筑面积和人口数都迅速增加.2014年中心城区住房建筑面积比2013年中心城区住房建筑面积增长的百分数是a,2015年中心城区住房建筑面积比2013年中心城区住房建筑面积增长的百分数是2a.从2014年开始,中心城区人口数在2013年180万的基础上每年递增m(m>0)万人,这样2015年中心城区的人口数比2014年中心城区人口数的1.5倍少80万人,已知2015年中心城区的人均住房建筑面积与2014年持平.
(1)根据题意填表(用含a,m的式子表示各个数量);
年份 | 中心城区人口数 | 中心城区人均住房建筑面积(单位:平方米) | 中心城区住房建筑面积(单位:万平凡米) |
2013年 | 180 | 30 | 5400 |
2014年 |
|
|
|
2015年 |
|
|
|
(2)求题目中的a和m.
查看答案和解析>>
科目:初中数学 来源: 题型:
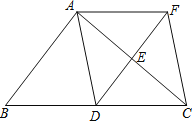
【题目】如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF.
(1)求证:四边形ADCF是平行四边形;
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com