
【题目】某一线城市对出租车营运价进行了调整,调价前后的收费标准对比如下:调整前,3公里及3公里以内12.5元,3公里后里程价2.4元/公里,无返空费;调整后, 2公里及2公里以内10元,2公里后里程价2.4元/公里,超过25公里部分,按里程价的30%加收返空费.
(1)请你帮忙计算一下,调价后,若乘客乘坐出租车的行程为8公里,他比以前少付了多少钱(不考虑红灯等因素)?
(2)网上流传“24公里换车”规避返空费,即乘客的行程超过25公里,就在24公里处下车,换乘另一辆出租车.但其实并不是所有行程超过25公里的乘客都需要换车.
例如:①若行程为30公里:不换车,总费用为:
10+23×2.4+5×2.4×130%=80.8元;
换车,总费用为:10+22×2.4+10+4×2.4=82.4元,因此,行程30公里若换车,则费用反而增加2.4元.
②若行程为40公里,不换车,总费用为:
10+23×2.4+15×2.4×130%=112元,若换车,总费用为:10+22×2.4+10+2.4×14=106.4元,则可节约5.6元.
若设行程为x 公里(26<x<48 ),请用含x的式子分别表示出不换车的费用和换车的费用,并帮忙计算一下,行程超过多少公里后换车会就会节约费用(不考虑红灯等因素).
【答案】(1)他比以前少付了0.1元;(2)行程超过![]() 公里后换车会就会节约费用.
公里后换车会就会节约费用.
【解析】试题分析:(1)调价前的付费为:起步价12.5+超过3公里的5公里的付费;调价后的付费为:起步价10+超过2公里的6公里的付费,两者相减,即可得到少付的费用;
(2)不换车的费用为:起步价10+2.4×超过2公里的23公里+2.4×130%×超过25公里的公里数;
换车的费用为:起步价10+2.4×超过2公里的22公里+起步价10+2.4×超过26公里的公里数;
让前面的代数式=后面的代数式求值即可.
试题解析:(1)调价前应付金额:12.5+(8-3) ×2.4=24.5 (元)
调价后应付金额:10+(8-2)×2.4=24.4 (元)
∴他比以前少付了24.5-24.4=0.1(元)
(2)不换车的费用10+(25-2)×2.4+(x-25)×2.4×(1+30%)=3.12x-12.8
换车的费用10+(24-2)×2.4+10+(x-26)×2.4=2.4x+10.4
令3.12x-12.8=2.4x+10.4
解得:x=![]()
由题意可知,当行程较短时,换车不节约费用,所以当行程超过![]() 公里后换车会节约费用.
公里后换车会节约费用.
答:行程超过![]() 公里后换车会节约费用.
公里后换车会节约费用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】观察下列各式及其验证过程: 验证: ![]() =
= ![]() ;
;
验证: ![]() =
= ![]() =
= ![]() =
= ![]() ;
;
验证: ![]() =
= ![]() ;
;
验证: ![]() =
= ![]() =
= ![]() =
= ![]() .
.
(1)按照上述两个等式及其验证过程的基本思路,猜想4 ![]() 的变形结果并进行验证;
的变形结果并进行验证;
(2)针对上述各式反映的规律,写出用n(n为任意自然数,且n≥2)表示的等式,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在仪仗队列中,共有八列,每列8人,若战士甲站在第二列从前面数第3个,可以表示为(2,3),则战士乙站在第七列倒数第3个,应表示为( )
A. (7,6) B. (6,7) C. (7,3) D. (3,7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药品经过两次降价,每瓶零售价由100元降为81元.已知两次降价的百分率都为x,那么x满足的方程是( )
A.100(1+x)2=81
B.100(1﹣x)2=81
C.100(1﹣x%)2=81
D.100x2=81
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知OA=3,OB=5,点D为y轴上一点,其坐标为(0,1),点P从点A出发以每秒1个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.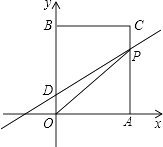
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD的面积S关于t的函数解析式;
②当点D关于OP的对称点落在x轴上时,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料: 解答“已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法:
解:∵x﹣y=2,又∵x>1,∴y+2>1,即y>﹣1
又y<0,∴﹣1<y<0.…①
同理得:1<x<2.…②
由①+②得﹣1+1<y+x<0+2,∴x+y的取值范围是0<x+y<2.
请按照上述方法,完成下列问题:
已知关于x、y的方程组 ![]() 的解都为非负数.
的解都为非负数.
(1)求a的取值范围;
(2)已知2a﹣b=1,且,求a+b的取值范围;
(3)已知a﹣b=m(m是大于1的常数),且b≤1,求2a+b最大值.(用含m的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com